05.3.1. Исследование функций и построение графиков. Признак монотонности функции

Одной из существенных характеристик функции являет­ся ее поведение на отдельных интервалах — возрастание или убывание. Это определяется приводимой ниже теоремой, дока­зательство которой мы опускаем.

ТЕОРЕМА 2. Если функция F (X) дифференцируема и f'(x) ≥ 0 (F'(X) ≤ 0) на интервале (а, b), то она не убывает (не возрас­тает) на этом интервале.

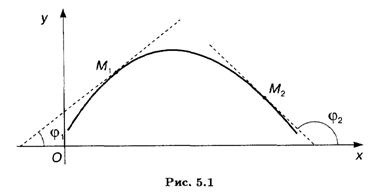
При F'(X) > 0 (F'(X) < 0) имеем признак строгой моно­тонности, т. е. функция возрастает (убывает). Геометрическая интерпретация связи знака производной функции и характера ее изменения очевидна (рис. 5.1): если углы наклона касатель­ных на каком-то интервале являются острыми, то функция на этом интервале возрастает: tg φ > 0; при тупом угле наклона касательной функция убывает и tg φ < 0.

Точки локального экстремума

Определение 1. Точка X0 называется точкой Локального мак­симума (минимума) функции F(X), если для любого Х ≠ x0 в не­которой окрестности точки X0 выполнено неравенство F(X0) > F(х) (F(X0) < F(X)).

Локальный минимум и локальный максимум объединены общим названием Локальный экстремум.

ТЕОРЕМА 3 (необходимое условие существования локаль­ного экстремума). Если функция F(X) дифференцируема в точке X0 и имеет в этой точке локальный экстремум, то f'(x0) = 0.

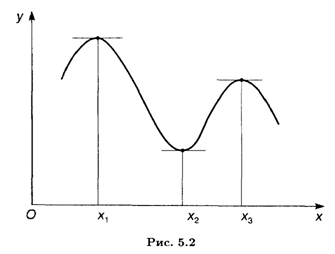
Геометрический смысл теоремы 5.3 указан на рис. 5.2: если в точках локальных экстремумов существуют касательные, то они параллельны оси Ох.

Точки, в которых касательные параллельны оси ОX, а зна­чит, производная равна нулю, называют Точками возможного экстремума, или стационарными точками. Если X0 — точка возможного экстремума, т. е. F'(X0) = 0, то она может и не быть точкой локального экстремума. Например, для функции F(X) = X3 (рис. 3.1) производная при Х = 0 равна нулю, од­нако в этой точке нет локального экстремума. Таким образом, теорема 5.3 не является достаточным условием существования локального экстремума.

ТЕОРЕМА 4 (достаточное условие существования локаль­ного экстремума). Пусть функция F(X) дифференцируема в некоторой окрестности точки x0. Если при переходе через точку x0 слева направо производная F'(X) меняет знак с плю­са на минус (с минуса на плюс), то в точке x0 функция F(X) имеет локальный максимум (минимум). Если же F'(X) не ме­няет знака в δ-окрестности точки x0, то данная функция не имеет локального экстремума в точке x0.

Рассмотрим применение доказанных теорем на примерах нахождения точек локальных экстремумов функций.

Пример 1. Найти точки локального экстремума и интервалы монотонности функции F(X) = Х3 — 7,5X2 + 18X.

Решение. Сначала находим производную F'(X) = 3X2 — 15X + 18. Приравнивая ее к нулю и решая уравнение Х2 — 5Х + 6 = 0, находим две точки возможного экстремума: X1 = 2 и X2 = 3. Нетрудно видеть, что F'(X) при переходе через точку X1 =2 меняет знак с "+" на "-", т. е. в этой точке имеет место локальный максимум; аналогично устанавливается, что в точке X2 = 3 функция F'(Х) имеет локальный минимум.

Найдем теперь интервалы монотонности данной функции (рис. 5.3). Поскольку F'(X) > 0 при Х (-,2), то в силу теоремы 5.2 функция монотонно возрастает на этом интер­вале; (2, 3) является интервалом монотонного убывания F(X) (F'(X) < 0), а на интервале (3, +) функция монотонно воз­растает (F'(X) > 0).

Пример 2. Найти размеры консервной банки, имеющей форму цилиндра (радиус R и высоту H) заданного объема V, при кото­рых полная поверхность сосуда будет минимальной. Эта зада­ча имеет производственный смысл: найти оптимальные разме­ры банки, при которых затраты материала на ее изготовление будут минимальны.

Решение. Исходя из формулы объема цилиндра V = πR2H, выразим H:

Как известно, полная поверхность цилиндра дается формулой

Подставляя сюда формулу для H, получаем S как функцию от R:

Минимум этой функции найдем из условия S' (R) = 0, от­куда получаем уравнение 2R — V / π R2 = 0. Из этого уравнения находим оптимальное значение R; его подставляем в формулу для H и окончательно вычисляем оптимальные размеры банки:

Например, при V = 0,33 л оптимальные размеры банки соста­вят: диаметр дна ≈ 7,5 см и высота ≈ 7,5 см.

< Предыдущая		Следующая >