04.1.3. Правая и левая производные

По аналогии с понятиями односторонних пределов функ­ции вводятся понятия правой и левой производных функции в точке.

Определение 3. Правой (левой) производной функции У = F(X) в точке X0 называется правый (левый) предел отноше­ния (4.1) при ΔX 0, если этот предел существует.

Для обозначения односторонних производных используется следующая символика:

Если функция F(X) имеет в точке X0 производную, то она имеет левую и правую производные в этой точке, которые сов­падают.

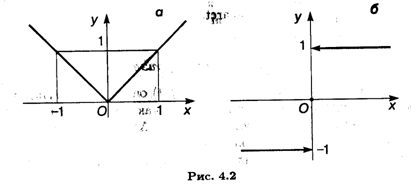
Приведем пример функции, у которой существуют одно­сторонние производные в точке, не равные друг другу. Это F(X) = |X|. Действительно, в точке Х = 0 имеем F’+(0) = 1, F'-(0) = -1 (рис. 4.2) и F’+(0) ≠ F’-(0), т. е. функция не имеет производной при Х = 0.

Операцию нахождения производной функции называют ее Дифференцированием; функция, имеющая производную в точ­ке, называется Дифференцируемой.

Связь между дифференцируемостью и непрерывностью функции в точке устанавливает следующая теорема.

ТЕОРЕМА 1. Если функция дифференцируема в точке X0, то она и непрерывна в этой точке.

Обратное утверждение неверно: функция F(X), непрерыв­ная в точке, может не иметь производную в этой точке. Таким примером является функция У = |X|; она непрерывна в точке X = 0, но не имеет производной в этой точке.

Таким образом, требование дифференцируемости функции является более сильным, чем требование непрерывности, по­скольку из первого автоматически вытекает второе.

< Предыдущая		Следующая >