03.5. Бесконечно малые и бесконечно большие функции
Определение 1. Функция F(X) называется Бесконечно малой функцией (или просто бесконечно малой) в точке X = А, если предел ее в этой точке равен нулю: ![]() F(X) = 0.
F(X) = 0.
Аналогично определяются бесконечно малые при Х ![]()
![]() , Х
, Х ![]() ±
±![]() , Х
, Х ![]() А+ и Х
А+ и Х ![]() а—.
а—.
ТЕОРЕМА 6. Алгебраическая сумма и произведение конечного числа бесконечно малых функций в точке а, как и произведение бесконечно малой на ограниченную функцию, являются бесконечно малыми функциями в точке а.
Определение 2. Функция F(X) называется Бесконечно большой Функцией в точке А (или просто бесконечно большой), если для любой сходящейся к А последовательности {хN} значений аргумента соответствующая последовательность {F(Xn)} значений функции является бесконечно большой.
В этом случае пишут ![]() F(X) =
F(X) = ![]() (
(![]() F(X) = +
F(X) = +![]() или
или ![]() F(X) = -
F(X) = -![]() ) и говорят, что функция имеет в точке А бесконечный предел (+
) и говорят, что функция имеет в точке А бесконечный предел (+![]() или -
или -![]() ). По аналогии с конечными односторонними пределами определены и односторонние бесконечные пределы:
). По аналогии с конечными односторонними пределами определены и односторонние бесконечные пределы:
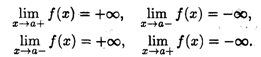
Аналогично определяются бесконечно большие функции при X![]()
![]() , X
, X![]() +
+![]() , X
, X![]() -
-![]() .
.
Между бесконечно малыми и бесконечно большими функциями существует та же связь, что и между соответствующими последовательностями, т. е. если α(х) — бесконечно малая функция при Х ![]() А, то F(X) = 1/α(х) — бесконечно большая функция, и наоборот.
А, то F(X) = 1/α(х) — бесконечно большая функция, и наоборот.
| < Предыдущая | Следующая > |
|---|