03.4. Два замечательных предела

В этом разделе приводятся два предела функции, которые наиболее широко используются в математике и ее приложени­ях. Доказательства соответствующих теорем мы опускаем.

ТЕОРЕМА 4. Предел функции в точке х =0 существу­ет и равен единице, т. е.

Предел (3.7) называется Первым замечательным пределом. Этот предел применяется при вычислении ряда других преде­лов. Рассмотрим несколько примеров на применение предела (3.7).

Пример 1. Найти предел функции sin (Ax) / Bx при Х 0.

Решение. Преобразуем данную дробь так, чтобы в знаме­нателе был аргумент синуса; только тогда можно будет при­менить первый замечательный предел, поскольку при Х 0 пределом Ах также является нуль. Получаем

Пример 2. Найти .

Решение. Теорему 3.2 здесь непосредственно применить нельзя, так как при Х 0 знаменатель дроби стремится к нулю. Для решения задачи необходимо сначала преобразовать данную дробь, а затем уже выполнить предельный переход:

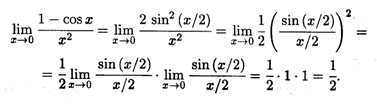
Пример 3. Найти .

Решение. Как и в первых двух примерах, преобразуем данную дробь, чтобы "подогнать" ее под первый замечательный предел:

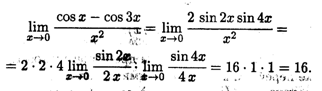
ТЕОРЕМА 5 (второй замечательный предел). Предел функции F(X) = при х существует и равен е, т. е.

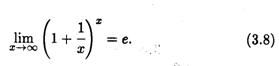
Число Е является одной из фундаментальных величин в ма­тематике. Показательная функция вида Е­­Ax называется Экспонентой, логарифм с основанием Е называется Натуральным и обозначается символом ln. В теории вероятностей и статистике функция является основополагающей.

Второй замечательный предел (3.8) широко применяется для вычисления других пределов. Рассмотрим примеры на его применение.

Пример 4. Найти .

Решение. Применим здесь замену переменной, полаем 1/X = У. Тогда У при X 0, т. е. имеем

Пример 5. Найти .

Решение. Заменим переменную, положив X = 2У. При X (а значит, и У ) последовательно получаем

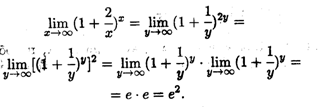
Пример 6. Найти .

Решение. Сначала преобразуем дробь под знаком предела, а затем уже перейдем к пределу:

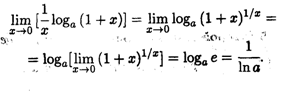
< Предыдущая		Следующая >