4.4. Сглаживание опытных данных методом наименьших квадратов (МНК)
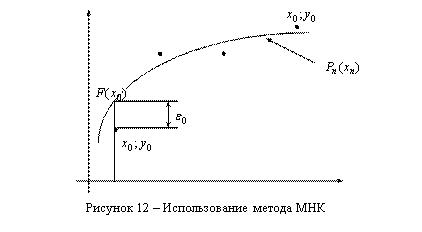
На практике чаще всего применяется другой метод аппроксимации опытных данных – МНК. Сущность метода состоит в том, что опытные данные аппроксимируются кривой ![]() , которая необязательно должна проходить через все узлы, а должна сгладить все случайные помехи табличной функции. При этом аппроксимирующую кривую
, которая необязательно должна проходить через все узлы, а должна сгладить все случайные помехи табличной функции. При этом аппроксимирующую кривую ![]() стремятся провести так, чтобы все ее отклонения от табличной функции (отклонения) были минимальными.
стремятся провести так, чтобы все ее отклонения от табличной функции (отклонения) были минимальными.
![]() ,
,
![]() ,
,
![]() .
.
Избавимся от знака отклонения: возведем его в квадрат.
![]() .
.
Для табличных данных, полученных в результате эксперимента, необходимо отыскать аналитическую зависимость кривой ![]() , сумма квадратов отклонений которой по всем узлам была бы минимальной.
, сумма квадратов отклонений которой по всем узлам была бы минимальной.
![]() .
.
Возьмем интерполяционный многочлен:
![]() .
.
Для определенности задачи будем выбирать функцию![]() из класса алгебраических многочленов. Степень многочлена
из класса алгебраических многочленов. Степень многочлена ![]() .
.
![]() .
.
Аппроксимирующий многочлен не проходит через все узлы, поэтому степень многочлена не зависит от количества узлов.
Как правило, в задаче степень аппроксимирующего многочлена задается, при этом всегда ![]() .
.
Если ![]() , то задача называется "линейная регрессия".
, то задача называется "линейная регрессия".
Если ![]() , то задача называется "квадратичная аппроксимация".
, то задача называется "квадратичная аппроксимация".
Если ![]() , то задача называется "кубическая аппроксимация".
, то задача называется "кубическая аппроксимация".
Уточним задачу аппроксимации.
Для табличных данных, полученных в результате эксперимента ![]() ,
, ![]() , необходимо построить аппроксимирующий многочлен
, необходимо построить аппроксимирующий многочлен ![]() , причем
, причем ![]() , для которого выполняется условие
, для которого выполняется условие
![]() . (15)
. (15)
Изменим вид многочлена:
![]() .
.
Перепишем условие (15):
![]() .
.
Необходимым условием существования минимума функции ![]() является равенство нулю ее частных производных:
является равенство нулю ее частных производных:
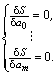
Дифференцируя ![]() по каждой переменной, получаем систему линейных уравнений:
по каждой переменной, получаем систему линейных уравнений:
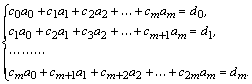 (16)
(16)
Порядок системы равен ![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() – коэффициенты аппроксимирующего многочлена (неизвестные).
– коэффициенты аппроксимирующего многочлена (неизвестные).
Решая полученную систему, определяем значения коэффициентов аппроксимирующего многочлена и в результате строим аппроксимирующий многочлен степени ![]() .
.
Для решения полученной системы (16) используем метод Гаусса. Перепишем систему (16):
 (17)
(17)
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() – коэффициенты многочлена вида
– коэффициенты многочлена вида
![]() . (18)
. (18)
Задача решается в следующем порядке:
1. Задается степень ![]() .
.
2. Строится система (17). Т. к. матрица коэффициентов симметрична относительно главной диагонали, то достаточно определить только наддиагональные элементы.
3. Решается система (17) методом Гаусса и находятся неизвестные коэффициенты аппроксимирующего многочлена.
4. Строится аппроксимирующий многочлен и определяется его значение в каждом узле.
5. Находится отклонение в каждой точке ![]() .
.
6. Находится сумма квадратов отклонений по всем узлам.
7. Рассчитывается остаточная дисперсия по формуле ![]() .
.
Для построения аппроксимирующего многочлена и вычисления его значений используем рациональную форму многочлена:
![]() . (19)
. (19)
Для вычисления значения многочлена в рациональной форме (19) удобно пользоваться схемой Горнера. В этом случае рекуррентная формула построения многочлена имеет вид:
![]() ,
, ![]() ,
, ![]() .
.
Выбор оптимального варианта аппроксимирующего многочлена, т. е. выбор его оптимальной степени ![]() , зависит от того, что мы положим в основу выбора критерия оптимальности. Можно положить в эту основу минимальные значения
, зависит от того, что мы положим в основу выбора критерия оптимальности. Можно положить в эту основу минимальные значения ![]() .
.
В этом случае поиск оптимальной степени ![]() будет вестись в пределах
будет вестись в пределах ![]() .
.
Окончательно ответить на вопрос, что должно быть положено в основу выбора критерия оптимальности многочлена, может только практика.
В данном случае это решение задач интерполяции или прогноза и сравнение результатов расчетов с результатами экспериментов.
| < Предыдущая | Следующая > |
|---|