4.3. Аппроксимация опытных данных
Проведен эксперимент, в результате которого получена табличная функция.
Таблица 3 – Точки табличной функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
: |
: |
|
|
|
|
![]() – координаты узловых точек.
– координаты узловых точек.
На графике функция представляется совокупностью узловых точек, их количество равно ![]() .
.
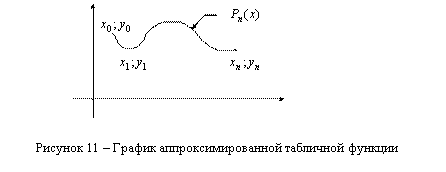
Необходимо для этих опытных данных решить задачу аппроксимации.
Сущность аппроксимации опытных данных состоит в нахождении аналитического выражения некоторой функции ![]() (аппроксимирующей кривой), которая приближала бы полученную табличную функцию.
(аппроксимирующей кривой), которая приближала бы полученную табличную функцию.
В настоящее время существуют два основных метода аппроксимации опытных данных: с помощью многочлена степени ![]() и методом наименьших квадратов.
и методом наименьших квадратов.
Аппроксимация опытных данных с помощью интерполяционного многочлена степени ![]() :
: ![]() . В этом случае аппроксимирующая кривая проходит через все узловые точки. Однако этот метод имеет недостатки:
. В этом случае аппроксимирующая кривая проходит через все узловые точки. Однако этот метод имеет недостатки:
1) точность аппроксимации гарантируется лишь в небольшом интервале ![]() при количестве точек не более 7–8.
при количестве точек не более 7–8.
2) значение функции в узлах должно быть задано с большой точностью. Однако известно, что как бы точно не проводился эксперимент, в результатах неизбежны погрешности.
Разброс результатов неизбежен в результате эксперимента. Дело в том, что наблюдаемая величина на самом деле зависит не только от того аргумента, который у нас в таблице, а ещё и от многих других случайных факторов (изменения температуры и давления окружающей среды, источников питания, погрешностей измерительных приборов, квалификации и самочувствия работников и т. д.). Многие из этих факторов меняются по своим собственным случайным законам, которые никак не связаны с интересующей нас функцией. Все это обуславливает случайную колеблемость снимаемой функции. В результате аппроксимировать опытные данные с помощью интерполяционного многочлена не всегда удается. Однако не всегда и нужно решать эту задачу с помощью интерполяционного многочлена. Стремясь пройти через все узлы и увеличивая при этом порядок многочлена, мы тем самым пытаемся воспроизводить не только закономерные изменения исследуемой функции, но и ее случайные помехи.
| < Предыдущая | Следующая > |
|---|