4.2. Построение интерполяционного многочлена по методу Ньютона

Пусть даны узлы –, а – значения функции или разделенные разности нулевого порядка. Тогда

,

– разделенные разности 1-го порядка;

,

– разделенные разности 2-го порядка.

Разделенная разность -го порядка для -й точки вычисляется через разделенную разность -го порядка:

.

Лемма.

Пусть произвольные попарно несовпадающие узлы, в которых известны значения функции . Тогда алгебраический многочлен -го порядка, который записывается в виде:

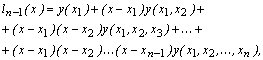
Является интерполяционным многочленом.

Например, .

Таблица 2 – Интерполяционный многочлен Ньютона

Интерполяционный многочлен Ньютона используется для неравных промежутков.

< Предыдущая		Следующая >