4.1. Построение интерполяционного многочлена по формуле Лагранжа
Для построения необходимо найти его коэффициенты ![]() .
.
Для нахождения коэффициентов необходимо построить систему линейных уравнений, которая может быть получена на основании того, что многочлен проходит через все узловые точки.
![]() .
.
В результате имеем систему:
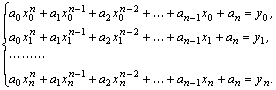
Порядок системы равен ![]() . Параметры
. Параметры ![]() ,
, ![]() известны и заданы в табличной функции. Неизвестными системы являются коэффициенты
известны и заданы в табличной функции. Неизвестными системы являются коэффициенты ![]() .
.
Далее полученный многочлен используется для решения задачи интерполирования.
Интерполяционный многочлен может быть построен и другими методами, например, при помощи специальных интерполяционных формул Лагранжа, Ньютона, Бесселя и др.
Интерполяционный многочлен по формуле Лагранжа имеет вид:
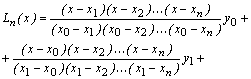

Многочлен ![]() является интерполяционным многочленом, т. е. в узловых точках он принимает значения таблицы.
является интерполяционным многочленом, т. е. в узловых точках он принимает значения таблицы.
Свернем формулу Лагранжа:
![]() , где
, где 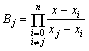 . (14)
. (14)
Алгоритм метода Лагранжа не предусматривает получение многочлена в явном виде, а сразу находит значение в промежуточных точках.
| < Предыдущая | Следующая > |
|---|