2.2. Метод Гаусса

В основе метода лежит идея последовательного исключения неизвестных. Процесс нахождения корней методом Гаусса состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно в обратном порядке находятся корни.

Для простоты рассмотрим систему 4-го порядка.

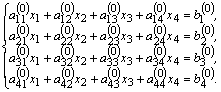(3)

Прямой ход (1-й шаг, ). Находим из 1-го уравнения системы (3) . – ведущий элемент первой строки. Если , то

.

Обозначив через , через , через через, получим

, (4)

Где и вычисляются по рекуррентным формулам:

Подставим выражение (4) для во 2-е, 3-е и 4-е уравнения системы (3). В результате получим:

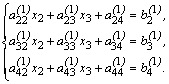(5)

вычисляются по рекуррентным формулам:

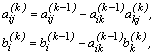
. (6)

В результате выполнения всех шагов прямого хода система (3) приводится к системе треугольного вида, которая получается объединением всех выражений для .

Начальная система принимает вид:

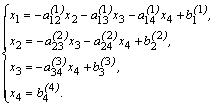(7)

Где .

Вычисления по всем шагам прямого хода при построении алгоритма организуем в цикле по . Последний, -й шаг прямого хода выводим из цикла, так как на этом шаге не нужны вычисления и , а реализуется только одно выражение . На каждом шаге прямого хода все преобразования коэффициентов и свободных членов проводятся по рекуррентным формулам (6).

В процессе обратного хода из системы (7) неизвестные находятся в обратном порядке (цикл по ). Используем рекуррентную формулу:

Далее, организуем поиск ненулевого ведущего элемента.

Рассмотренный простейший метод Гаусса называется схемой единственного деления. Он обладает следующим недостатком: если ведущий элемент какой-либо строки () окажется равным , то этот метод формально непригоден, хотя система может иметь решение. Поэтому в схеме алгоритма необходимо добавить блок поиска ненулевого ведущего элемента. Суть поиска следующая: если в какой-либо строке имеется нулевой ведущий элемент , то в этом же -м столбце в цикле по осуществляется поиск ненулевого элемента. Если в строке этого столбца такой элемент найден, то строки и меняются местами.

< Предыдущая		Следующая >