2.1. Решение систем линейных уравнений (СЛУ)

Если прикладная система имеет несколько степеней подвижности, а физические процессы, протекающие в ней линейны, то математическая модель такой системы описывается с помощью системы линейных уравнений.

Например, с помощью систем линейных уравнений в математике часто описываются математические задачи планирования и управления, в механике - статически неопределимые системы.

Часто при решении прикладных задач нелинейные процессы приходится линеаризировать.

В общем виде система линейных уравнений имеет вид:

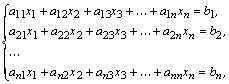
Где – коэффициенты системы, – свободные члены, – неизвестные, – номер строки, – номер столбца, – порядок.

В матричной форме СЛУ имеет вид:,

Где

, , .

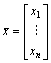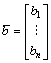Численные методы решения СЛУ можно разбить на две группы:

1) точные (прямые) методы;

2) приближенные (итерационные) методы.

Методы первой группы позволяют получить решение за конечное число арифметических действий. К этим методам относятся: правило Крамера, метод Гаусса (исключений), метод прогонки.

Методы второй группы реализуют на ЭВМ. Нахождение корней с заданной степенью точности.

< Предыдущая		Следующая >