18. Інтеграл Дюамеля

Згідно теореми множення зображень (3.2):

Якщо , а , то маємо

.

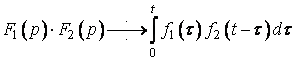Визначимо оригінал, що відповідає добутку

,

Використовуючи теорему (2.7) диференціювання оригіналів. Запишемо цей добуток у вигляді

.

Тоді одержимо

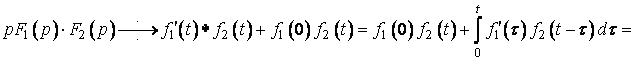
. (29)

Формула (29) називається інтегралом Дюамеля.

Якщо в формулі (29) поміняти місцями зображення , а значить, і оригінали , то одержимо формулу

. (30)

При одержанні формули (30) використана властивість комутативності згортки.

Інтеграл Дюамеля використовують при розв’язанні диференціальних рівнянь операційним методом.

Приклад 25. Знайти оригінал функції

.

Розв’язання.

.

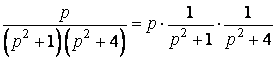Так як 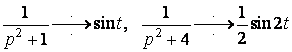, то за формулою (29) маємо

.

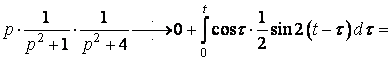
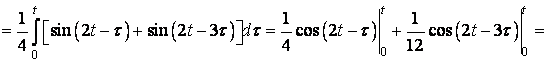
< Предыдущая		Следующая >