10. Диференціювання оригіналу

Якщо функція є оригіналом з показником зростання , причому , і існує похідна , що також являється оригіналом, з тим же показником зростання , то

, (20)

де .

Повторне застосування теореми дає:

(21)

Якщо - неперервні, а − кусково неперервна на , є оригіналами з одним і тим же показником зростання і , то

. (22)

Приклад 13. Знайти зображення за теоремою 2.7.

Розв’язання. 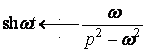і , то за формулою (20) маємо:

,

.

< Предыдущая		Следующая >