11. Інтегрування оригіналу

Якщо функція є оригіналом, причому , то 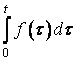також є оригіналом і

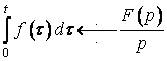. (23)

Таким чином, інтегруванню оригіналу відповідає ділення його зображення на .

Приклад 14. Знайти зображення функції

.

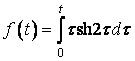Розв’язання. За формулою (7) .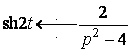

Використовуючи формулу (17), одержимо

.

.

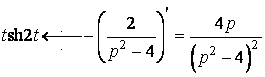Приклад 15. Користуючись теоремою (2.8) інтегрування оригіналу, знайти оригінал за зображенням

.

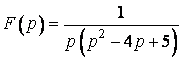Розв’язання. Перетворимо це зображення до однієї з відомих формул. Виділимо повний квадрат:

.

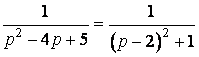За формулою (13) можна записати

.

За формулою (23) маємо:

.

< Предыдущая		Следующая >
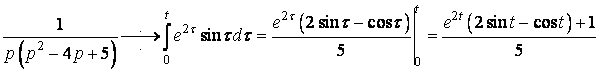