08. Теорема диференціювання зображення

Якщо , то

, (17)

Тобто диференціюванню зображення відповідає множення оригіналу на .

Застосовуючи операцію диференціювання зображення багаторазово, можна показати, що

. (18)

За допомогою цієї теореми легко знайти зображення функції :

. (19)

Приклад 9. Знайти зображення функції

.

Розв’язання.

, .

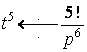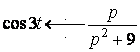За теоремою зміщення маємо

.

За формулою 17 маємо

.

Користуючись теоремою лінійності, одержимо

.

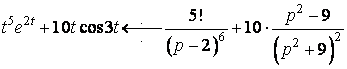Приклад 10. Знайти зображення функції

.

Розв’язання.

.

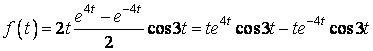За формулою (13) маємо

.

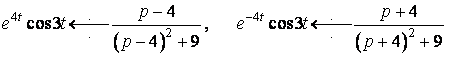Скориставшись теоремою диференціювання зображення, одержимо

,

,

.

Зауваження В деяких випадках буває необхідним знайти зображення

для дробового .

Це можна зробити так:

,

де .

Гамма – функція визначається, як інтеграл

.

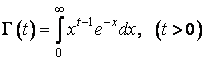Тоді .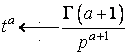

При цілому :

Приклад 11. Знайти зображення функцій .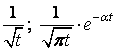

Розв’язання.

.

Використовуючи останній результат і теорему зміщення , одержимо

.

< Предыдущая		Следующая >