07. Теорема запізнення
Розглянемо оригінал ![]() . Тоді функція
. Тоді функція
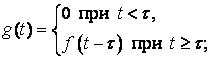
де ![]() - додатнє число, має графік, який одержується із графіка
- додатнє число, має графік, який одержується із графіка ![]() зсувом останнього на величину
зсувом останнього на величину ![]() в додатному напрямку осі
в додатному напрямку осі ![]() (Рис. 3)
(Рис. 3)
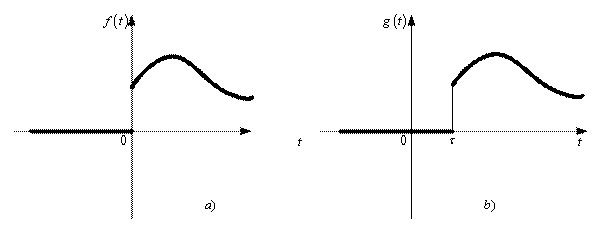
Рис. 3
Якщо функція ![]() визначає перебіг у часі якогось процесу, то функція
визначає перебіг у часі якогось процесу, то функція ![]() визначає той же процес, що почався з запізненням
визначає той же процес, що почався з запізненням ![]() .
.
Якщо ![]() - одинична функція Хевісайда, то графік функції
- одинична функція Хевісайда, то графік функції ![]() має вигляд, зображений на рисунку 4.
має вигляд, зображений на рисунку 4.

Рис. 4
За допомогою одиничної функції Хевісайда функцію ![]() , що запізнюється на
, що запізнюється на ![]() , можна записати так:
, можна записати так:
![]() ,
,
Бо ![]() (в цьому випадку аргумент від'ємний) і 1 при
(в цьому випадку аргумент від'ємний) і 1 при ![]() .
.
Теорема. Якщо ![]() і
і ![]() - будь-яке додатнє число, то
- будь-яке додатнє число, то
![]() . (16)
. (16)
Виходячи із фізичного тлумачення, теорему запізнення можна сформулювати так: запізненню оригіналу на час ![]() відповідає множення зображення на
відповідає множення зображення на ![]() .
.
На цій теоремі буде засновано зображення багатьох функцій (частково функцій, які описують імпульсні процеси).
Застосуємо теорему запізнення до побудови зображення одиничного імпульсу ![]() , що діє за проміжок часу
, що діє за проміжок часу ![]()

Графік його зображено на рисунку 5.
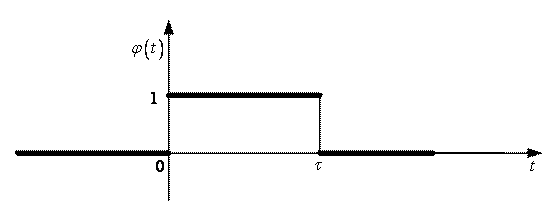
Рис. 5
Цей одиничний імпульс можна розглядати, як різницю двох оригіналів: одиничної функції і одиничної функції, що зсунена на ![]() . Запишемо
. Запишемо ![]() за допомогою одиничної функції Хевісайда:
за допомогою одиничної функції Хевісайда:
![]() .
.
Застосовуючи теореми лінійності і запізнення, одержимо
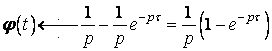 .
.
Нехай тепер одиничний імпульс починається не в момент ![]() , а в деякий момент
, а в деякий момент ![]() і, як і раніше, діє за проміжок часу
і, як і раніше, діє за проміжок часу ![]() (Рис. 6).
(Рис. 6).
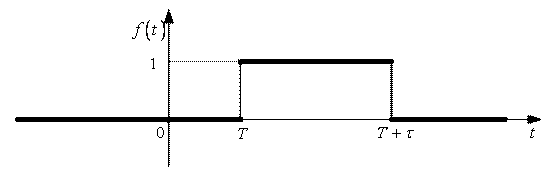
Рис. 6
![]() .
.
Застосовуючи теорему запізнення, одержимо його зображення:
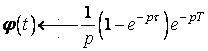 .
.
Приклад 4. Знайти зображення оригіналу
![]() .
.
Розв’язання. ![]() є функція
є функція ![]() , яка "вмикається" з запізненням
, яка "вмикається" з запізненням ![]() .
.
 .
.
За теоремою запізнення маємо
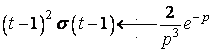 .
.
Якщо б ми не написали множник ![]() , то одержали б функцію
, то одержали б функцію ![]() , яка означає оригінал
, яка означає оригінал ![]() без запізнення. Зображення цього оригіналу буде
без запізнення. Зображення цього оригіналу буде
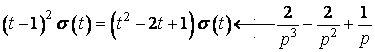 .
.
Приклад 5. Знайти зображення функції
![]() .
.
Розв’язання. Функція ![]() описує деякий процес, що "вмикається" із запізненням
описує деякий процес, що "вмикається" із запізненням ![]() . Щоб вирішити, який це процес, треба задану функцію записати у формі
. Щоб вирішити, який це процес, треба задану функцію записати у формі
![]() .
.
Зробимо це:
![]()
![]() .
.
Отже, ![]() є процес
є процес ![]() , що "вмикається" із запізненням
, що "вмикається" із запізненням ![]() .
.
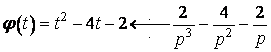 .
.
Застосовуючи теорему запізнення, одержимо
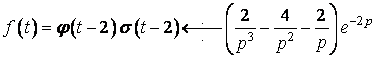 .
.
Приклад 6. Знайти зображення функцій ![]() і
і ![]() , заданих на рисунках 7 (а і б).
, заданих на рисунках 7 (а і б).

Рис. 7
Розв’язання. Перша функція є імпульс величини 3, що вмикається в момент часу ![]() і "гасне" в момент
і "гасне" в момент ![]() . Отже,
. Отже,
![]() .
.
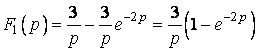 .
.
![]() .
.
 .
.
Приклад 7. Знайти зображення функції, заданої на рисунку 8.

Рис. 8
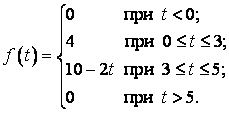
Розв’язання. Задамо функцію аналітично
1) ![]() ,
,
2) на інтервалі ![]() скористуємося рівнянням прямої, що проходить через дві дані точки
скористуємося рівнянням прямої, що проходить через дві дані точки ![]() та
та ![]() :
:
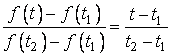 .
.
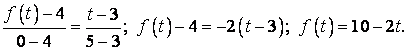
3) ![]() .
.
Отже,
За допомогою одиничної функції Хевісайда запишемо ![]() одним аналітичним виразом.
одним аналітичним виразом.
![]() , в момент
, в момент ![]() "вмикається" функція, що дорівнює 4; в момент
"вмикається" функція, що дорівнює 4; в момент ![]() вона "гасне" і "вмикається" функція
вона "гасне" і "вмикається" функція ![]() ; в момент
; в момент ![]() "гасне" і ця функція. Всю цю послідовність можна записати так:
"гасне" і ця функція. Всю цю послідовність можна записати так:
![]()
![]() .
.
Щоб знайти зображення цієї функції, треба подати її в формі:
![]() .
.
Маємо
![]() .
.
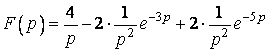 .
.
Зауваження. Якщо функція ![]() задана так:
задана так:
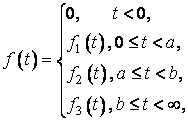
То за допомогою одиничної функції Хевісайда її можна записати одним аналітичним виразом:
![]() .
.
Приклад 8. Знайти оригінал за його зображенням
 .
.
Розв’язання.
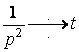 .
.
Застосовуючи теорему запізнення, одержимо
![]() .
.
| < Предыдущая | Следующая > |
|---|