06. Теорема зміщення

Якщо - оригінал і , то для будь-якого дійсного або комплексного числа

, (12)

Тобто множенню оригіналу на функцію відповідає "зміщення" аргументу зображення на .

Скориставшись теоремою зміщення, одержимо зображення функцій:

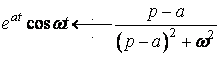(13)

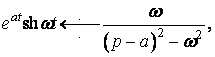
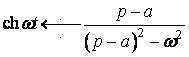(14)

Часто виявляються корисними формули відповідності для добутку оригіналу на або . Застосовуючи теореми зміщення та лінійності, одержимо формули

, (15)

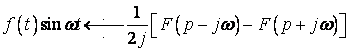. (16)

Аудиторне заняття 1. (АЗ-1)

1. Перевірити які з заданих функцій є функціями – оригіналами:

.

2. Користуючись визначенням, знайти зображення функцій .

3. Знайти зображення наступних оригіналів:

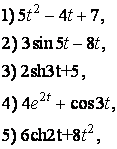
4. Знайти зображення функцій:

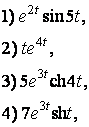
5. Знайти оригінал за зображенням:

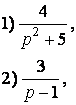
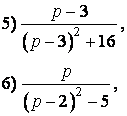
Самостійна робота.

1. Знайти зображення функцій.

2. Знайти оригінали.

Варіант 1.

Варіант 2.

Варіант 3.

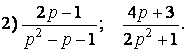
< Предыдущая		Следующая >