02. Оригінали і зображення. Основні визначення
Визначення 1. Оригіналом ми будемо називати любу комплексну функцію ![]() дійсного аргументу
дійсного аргументу ![]() , якщо вона задовольняє три умови:
, якщо вона задовольняє три умови:
а) функція ![]() і її похідна
і її похідна ![]() на любому кінцевому проміжку осі
на любому кінцевому проміжку осі ![]() мають не більше кінцевої кількості точок розриву першого роду;
мають не більше кінцевої кількості точок розриву першого роду;
б) функція ![]() при
при ![]() ;
;
в) існують такі сталі ![]() і
і ![]() , що
, що ![]() .
.
Умова а) означає, що будь-який скінченний інтервал осі ![]() можна розбити на скінченне число таких інтервалів, в кожному з яких
можна розбити на скінченне число таких інтервалів, в кожному з яких ![]() і
і ![]() неперервні і в кінцевих точках цих інтервалів мають скінченні ліві і праві границі.
неперервні і в кінцевих точках цих інтервалів мають скінченні ліві і праві границі.
Отже, оригінали ні при яких ![]() не перетворюються в нескінченність. Так функція
не перетворюються в нескінченність. Так функція ![]() і функція
і функція ![]() не є оригіналами й з розгляду вилучаються.
не є оригіналами й з розгляду вилучаються.
Умова б), яка вимагає рівності оригіналу нулю при ![]() , практично не є обмежливою, бо при розв’язанні диференціальних рівнянь, відповідних фізичним задачам (а для цього, взагалі, і будується операційне числення), нас цікавлять значення функцій, заданих початковими умовами, які завжди можна прийняти за момент
, практично не є обмежливою, бо при розв’язанні диференціальних рівнянь, відповідних фізичним задачам (а для цього, взагалі, і будується операційне числення), нас цікавлять значення функцій, заданих початковими умовами, які завжди можна прийняти за момент ![]() .
.
На практиці ми будемо записувати лише той вираз оригіналу ![]() , який він має при
, який він має при ![]() , але слід пам’ятати про умову б). Тобто, якщо написано
, але слід пам’ятати про умову б). Тобто, якщо написано ![]() , то це слід розуміти так:
, то це слід розуміти так:
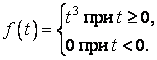
Надалі під значенням оригіналу ![]() при
при ![]() будемо розуміти праву границю:
будемо розуміти праву границю:
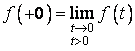 .
.
Умова в) накладає обмеження на характер зростання оригіналу ![]() , тобто вимагає, щоб
, тобто вимагає, щоб ![]() при
при ![]() зростала не швидше показникової функції
зростала не швидше показникової функції ![]() .
.
Число ![]() з умови в) будемо називати показником зростання
з умови в) будемо називати показником зростання ![]() . Отже, наприклад, функція
. Отже, наприклад, функція
![]()
Не є оригіналом, бо при ![]() вона зростає бистріше, чим дозволяє умова в).
вона зростає бистріше, чим дозволяє умова в).
Більшість функцій, що зустрічаються на практиці, задовольняють умовам (а - в).
Визначення 2. Зображенням функції ![]() називають функцію
називають функцію![]() комплексної змінної
комплексної змінної ![]() , визначену співвідношенням
, визначену співвідношенням
 . (1)
. (1)
Інтеграл в правій частині цієї рівності називають інтегралом Лапласа для функції ![]() . Операцію переходу від оригіналу
. Операцію переходу від оригіналу ![]() до зображення
до зображення ![]() називають перетворенням Лапласа. Речення "оригінал
називають перетворенням Лапласа. Речення "оригінал ![]() має зображення
має зображення ![]() " записують символічно так:
" записують символічно так:
![]()
(стрілка направлена завжди від зображення до оригіналу).
Приклад 1. Знайти зображення одиничної функції Хевісайда (Рис. 1)
 (2)
(2)

Рис. 1
Розв’язання. Функція ![]() є оригіналом тому, що виконуються три умови а), б), в). В умові в) для цієї функції
є оригіналом тому, що виконуються три умови а), б), в). В умові в) для цієї функції ![]() .
.
Користуючись визначенням (2), знаходимо
 ,
,
Причому останній висновок можна зробити тільки в тому випадку, коли ![]() . Якщо
. Якщо ![]() , то
, то ![]()
![]() і
і ![]() .
.
Отже,
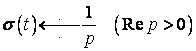 . (3)
. (3)
Приклад 2. Знайти зображення функції

де ![]() - комплексне число.
- комплексне число.
Розв’язання. Ця функція неперервна при ![]() і обмежена, тобто є оригіналом.
і обмежена, тобто є оригіналом.
 ,
,
якщо тільки ![]() .
.
Останнє має місце при ![]() , або
, або ![]() (тобто правіше прямої
(тобто правіше прямої ![]() )
)
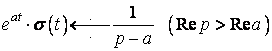 . (4)
. (4)
Роль множника ![]() в лівій частині (4) полягає в тому, що він гасить (обертає в нуль) функцію при
в лівій частині (4) полягає в тому, що він гасить (обертає в нуль) функцію при ![]() .
.
Надалі будемо вважати, що всі функції, які розглядаються, мають множник ![]() , але сам множник не будемо записувати. Наприклад, можна писати
, але сам множник не будемо записувати. Наприклад, можна писати ![]() і т. д., розуміючи при цьому відповідно
і т. д., розуміючи при цьому відповідно ![]() і т. д.
і т. д.
| < Предыдущая | Следующая > |
|---|