06. Вероятность попадания непрерывной случайной величины в заданный интервал
Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.
Теорема: Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащие интервалу (A,B), равна определённому интегралу от плотности распределения, взятому в пределах от A до B :
 .
.
Доказательство: Используем соотношение
P(A ≤ X< B) = F(B) – F(A).
По формуле Ньютона-Лейбница,
 .
.
Таким образом,
 .
.
Так как P(A ≤ X < B)=P(A < X < B), то окончательно получим
 .
.
Геометрически полученный результат можно истолковать так : Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (A,B), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения F(X) и прямыми X = A и X = B.
Замечание: В частности, если F(X) – чётная функция и концы интервала симметричны относительно начала координат, то
 .
.
Пример. Задана плотность вероятности случайной величины Х

Найти вероятность того, что в результате испытания Х примет значение, принадлежащие интервалу (0,5; 1).
Решение: Искомая вероятность
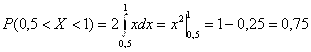 .
.
| < Предыдущая | Следующая > |
|---|