04. Закон распределения вероятностей дискретной случайной величины
Определение3.1:Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Способы задания дискретной случайной величины
1) Для задания дискретной случайной величины достаточно задать семейство вероятностей Pi = P(X = Xi), Где ![]() Или
Или ![]() .
.
2) Задать закон распределения дискретной случайной величины можно в виде функции распределения вероятностей (интегральной функции распределения) F(X), Где
F(X) = P(X < X) = P(![]() ) =
) = ![]() .
.
Замечание: Воспользовались теоремой сложения для несовместных событий.
Получили, что
F(x) =![]() , Где Pi = P(X = xi) = F(xi+0) - F (xi).
, Где Pi = P(X = xi) = F(xi+0) - F (xi).
График функции распределения дискретной случайной величины имеет ступенчатый вид:
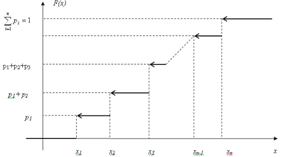
3) Ряд распределения или табличный способ задания дискретной случайной величины: первая строка таблицы содержит возможные значения случайной величины, расположенные в порядке возрастания, а вторая – их вероятности:
|
X |
x1 |
X2 |
X3 |
….. |
|
Xn |
|
P |
p1 |
P2 |
P3 |
….. |
|
Pn |
Сумма вероятностей второй строки таблицы равна единице:
![]() (условие нормировки).
(условие нормировки).
Замечание1: В одном испытании случайная величина X принимает одно и только одно возможное значение, следовательно, события (X = Xi), где ![]() образуют полную группу.
образуют полную группу.
Замечание2: Если множество возможных значений бесконечно (счетно), то ряд ![]() Сходится и его сумма равна единице.
Сходится и его сумма равна единице.
4) Многоугольник распределения или графический способ задания дискретной случайной величины.
В прямоугольной системе координат строят точки ( Xi, Pi ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 10000 рублей и десять выигрышей по 1000 рублей. Найти ряд распределения, функцию распределения случайной величины X – Стоимости возможного выигрыша для владельца одного лотерейного билета. Построить многоугольник распределения.
Решение: Случайная величина X принимает значения 0,1000,10000 с вероятностями:
![]() ,
, ![]() ,
, ![]() .Таким образом, ряд распределения имеет следующий вид:
.Таким образом, ряд распределения имеет следующий вид:
|
X |
0 |
1000 |
10000 |
|
P |
0,89 |
0,1 |
0,01 |
Условие нормировки выполняется: ![]() .
.
Найдем функцию распределения данной случайной величины X :
Если X ≤ 0 , То F(X) = 0 (третье свойство). Если 0 < X ≤ 1000 , То F(X) = 0,89. Действительно, X может принять значение 0 с вероятностью 0,89. Если 1000 < X ≤ 10000 , То F(X) = 0,99.
Действительно, если X1 удовлетворяет неравенству 1000 < X1 ≤ 10000 , То F(X1) Равно вероятности события X < X1 , которое может быть осуществлено, когда X примет значение 0 с вероятностью 0,89 Или 1000 с вероятностью 0,1. Поскольку эти два события несовместны, то по теореме сложения вероятность события X < X1 равна сумме вероятностей 0,89 + 0,1 = 0,99.
Если X >10000 , То F(X) = 1 (третье свойство). Итак, функция распределения аналитически может быть записана следующим образом:
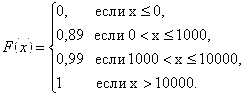
График функции распределения:
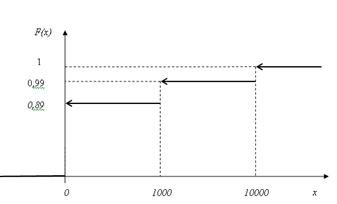
Многоугольник распределения имеет следующий вид:
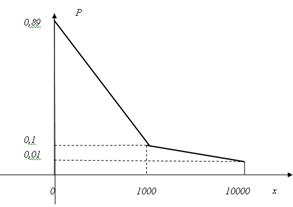
| < Предыдущая | Следующая > |
|---|