4.13. Интегрирование линейных дифференциальных уравнений с помощью степенных рядов

Если коэффициенты линейного дифференциального уравнения являются аналитическими функциями, т. е. представимы в виде степенных рядов, то решение уравнения можно искать в виде степенного ряда с неопределенными коэффициентами . Для этого разложим коэффициенты уравнения также в степенные ряды и подставим искомое решение, получим уравнение для коэффициентов , которые отыскивается методом неопределенных коэффициентов.

Рассмотрим применение метода на примерах.

1. Найти общее решение уравнения Эйри .

Ищем решение в виде степенного ряда :

.

Приравниваем коэффициенты при одинаковых степенях :

Отсюда следует . Из этой системы равенств имеем

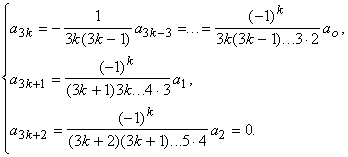
Полагая сначала , найдем

(1)

Затем , получим

(2)

По признаку Даламбера сходимости рядов легко устанавливается интервал сходимости этих рядов - он равен .

Покажем теперь, что функции и являются линейно независимыми частными решениями уравнения Эйри (1). Предположим противное при . Положим . Следовательно, должно выполняться равенство . Тогда имеем , а это противоречит условию .

Итак, решения и образуют фундаментальную систему решений уравнения (1). Общее решение уравнения Эйри имеет вид:

,

Где и - произвольные постоянные.

2. Найти общее решение уравнения .

Ищем решение в виде : .

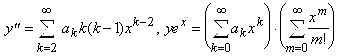Ограничимся, например, пятью членами разложения в экспоненте:

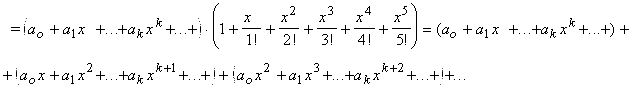
Приравниваем коэффициенты при одинаковых степенях :

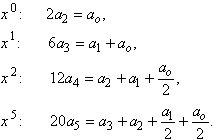
Отсюда следует .

Подставив эти значения в функцию И переобозначим , имеем общее решение

,

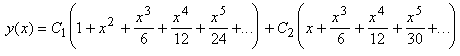Где и - произвольные постоянные.

< Предыдущая