4.10. Метод вариации произвольной постоянной
Рассмотрим ЛНДУ n-го порядка
![]() . (1)
. (1)
Согласно теореме о структуре решения ЛНДУ его решение есть
![]() (2)
(2)
Предположим, что известно решение ЛОДУ ![]() . Для нахождения частного решения
. Для нахождения частного решения ![]() будем считать постоянные
будем считать постоянные ![]() функциями
функциями ![]() , т. е.
, т. е.
![]() . (3)
. (3)
Найдем производную
![]() (4)
(4)
И выберем ![]() так, чтобы
так, чтобы ![]() . Найдем вторую производную
. Найдем вторую производную
![]() (5)
(5)
И положим ![]() . Найдем третью производную и т. д.
. Найдем третью производную и т. д. ![]() раз. Подставим найденные производные
раз. Подставим найденные производные ![]() и функцию (3) в уравнение (1), найдем
и функцию (3) в уравнение (1), найдем 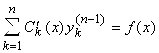 . В результате построим систему неоднородных уравнений линейных уравнений относительно функций :
. В результате построим систему неоднородных уравнений линейных уравнений относительно функций :

Определителем этой системы является определитель Вронского ![]() , который отличен от нуля, т. к. система решений
, который отличен от нуля, т. к. система решений ![]() является фундаментальной системой решений. Поэтому система имеет единственное решение
является фундаментальной системой решений. Поэтому система имеет единственное решение ![]() . Интегрируя эти соотношения, найдем
. Интегрируя эти соотношения, найдем ![]() . После подстановки этих функций в (3) находим окончательно
. После подстановки этих функций в (3) находим окончательно
 , (7)
, (7)
Где ![]() ,
, ![]() - произвольные постоянные.
- произвольные постоянные.
Пример. Найти общее решение уравнения ![]() .
.
Решим сначала однородное уравнение ![]() . Заметим, что
. Заметим, что ![]() . Откуда
. Откуда ![]() или
или ![]() . Еще раз интегрируем, получим
. Еще раз интегрируем, получим ![]() .
.
Считаем, что ![]() . Составим систему
. Составим систему
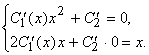
Откуда ![]() или
или ![]() .
.
Общее решение уравнения
![]()
| < Предыдущая | Следующая > |
|---|