4.08. Формула Остроградского-Лиувилля

Теорема 1. Если система функций является фундаментальной системой решений ЛОДУ

(1)

На некотором интервале, то определитель Вронского этой системы вычисляется по формуле

. (2)

В частности, для задачи Коши

, (3)

Где - произвольная постоянная, .

Доказательство.

Запишем определитель Вронского фундаментальной системой решений и его производную

.

Заметим, что эти определители отличаются только последней строкой. Выразим из уравнения (1) и подставим в определитель . Используем свойства определителей:

1) ;

2) определитель, имеющий строки, отличающиеся на постоянный множитель, равен нулю.

После преобразований найдем

.

Интегрируя это уравнение, получим (2).

В случае задачи Коши постоянная интегрирования находится из начального условия . Откуда и имеем формулу (3).

Теорема 2. Если известно одно частное решение ЛОДУ второго порядка , то общее решение выражается формулой

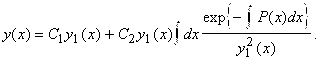(4)

Доказательство.

По формуле Остроградского-Лиувилля

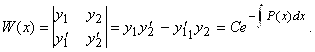
Мы получили дифференциальное уравнение 1-го порядка относительно функции . Разделив уравнение на , имеем

Нас интересует частное решение, поэтому полагаем . Тогда общее решение исходного уравнения запишется в виде (4).

Пример. В уравнении известно частное решение . Для нахождения второго частного решения вычислим интеграл . Тогда, общее решение имеет вид

.

< Предыдущая		Следующая >