Глава 07. Законы распределения наработки до отказа: экспоненциальный, логнормальный и гамма-распределение. Экспоненциальное распределение
Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний (выходного контроля) отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации.
Эти объекты можно отнести к «не стареющим», поскольку они работают только на участке с ![]() (t) =
(t) = ![]() = const. Круг таких объектов широк: сложные технические системы с множеством компонентов, средства вычислительной техники и системы автоматического регулирования и т. п. Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов.
= const. Круг таких объектов широк: сложные технические системы с множеством компонентов, средства вычислительной техники и системы автоматического регулирования и т. п. Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов.
Считается, что случайная величина наработки объекта до отказа подчинена экспоненциальному распределению, если ПРО описывается выражением:
|
F(t) = |
(1) |
где ![]() – параметр распределения, который по результатам испытаний принимается равным
– параметр распределения, который по результатам испытаний принимается равным
![]()
![]() 1 /
1 / ![]() 0 ,
0 ,
Где ![]() 0 – оценка средней наработки до отказа.
0 – оценка средней наработки до отказа.
Остальные показатели безотказности при известной F(t), определяются:
|
- Вероятность безотказной работы (ВБР): |
P(t) = exp ( - |
(2) |
|
- Вероятность отказа (ВО): |
Q(t) = 1 - exp ( - |
(3) |
|
- Интенсивност отказов (ИО): |
|
(4) |
Из (4) следует, что ИО является постоянной величиной, не зависящей от времени, и обратно пропорциональной оценке средней наработки ![]() (t) =
(t) = ![]() = 1/
= 1/ ![]() 0 .
0 .
Числовые характеристики наработки до отказа определяются:
- Средняя наработка (МО наработки) до отказа
|
|
(5) |
- Дисперсия наработки до отказа
|
|
(6) |
Графики изменения показателей безотказности при экспоненциальном распределении приведены на рис. 1.
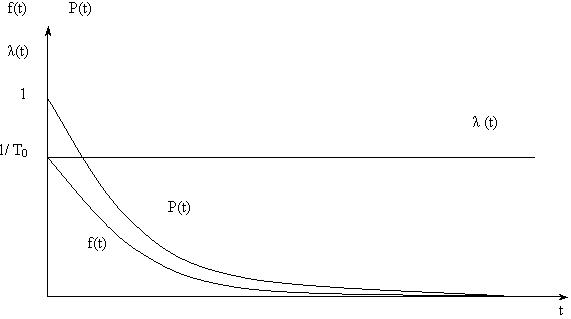
Рис. 7.1
Следует отметить, что при ![]() T < < 1, т. е. при наработке t много меньшей, чем средняя наработка T0, выражения (1) – (4) можно упростить, заменив e-
T < < 1, т. е. при наработке t много меньшей, чем средняя наработка T0, выражения (1) – (4) можно упростить, заменив e-![]() T двумя первыми членами разложения e-
T двумя первыми членами разложения e-![]() T в степенной ряд.
T в степенной ряд.
Например, выражение для ВБР примет вид:
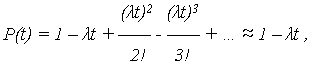
при этом погрешность вычисления P(t) не превышает 0,5 (![]() T)2.
T)2.
Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надежности «стареющих» объектов, подверженных износовым отказам.
| < Предыдущая | Следующая > |
|---|