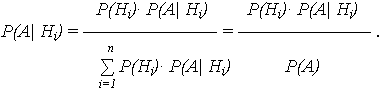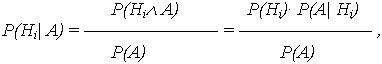Глава 02.5. Следствия основных теорем

 Следствия основных теорем - формула полной вероятности (ФПВ) и формула Байеса находят широкое применение при  решении большого числа задач.

Формула полной вероятности.

Если по результатам опыта можно сделать N исключающих друг друга предположений (гипотез) H1, H2, … Hn, представляющих полную группу несовместных событий (для которой  P(i)=1), то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:

(13)

Где P(Hi) – вероятность гипотезы Hi;

P(А| Hi) – условная вероятность события А При гипотезе Hi.

Поскольку событие А может появиться с одной из гипотез H1, H2, … Hn, то  А= АH1 АH2 … АHn  , но  H1, H2, … Hn несовместны, поэтому

 

 При зависимости события А от появления гипотезы Hi  P(AHi) = P(Hi)· P(А| Hi), откуда и следует выражение (13).

Формула Байеса (формула вероятностей гипотез).

Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …, P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:

(14)

 Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называются Априорными, а послеопытные - P(H1| А), … P(Hn| А) – Апостериорными.

Формула Байеса позволяет «пересмотреть» возможности гипотез с учетом полученного результата опыта.

Доказательство формулы Байеса следует из предшествующего материала. Поскольку P(Hi А) = P(Hi)· P(А| Hi) = P(Hi)· P(Hi| А):

(15)

 откуда, с учетом (13), получается выражение (15).

Если после опыта, давшего событие А, проводится еще один опыт, в результате которого может произойти или нет событие А1, то условная вероятность этого последнего события вычисляется по (13), в которую входят не прежние вероятности гипотез P(Hi), а новые - P(Hi| А):

(16)

 Выражение (16) называют Формулой для вероятностей будущих событий.

< Предыдущая		Следующая >