Глава 14.3. Модели процессов приближения объекта к отказам. Основные классы моделей

Как отмечалось ранее, основой случайных процессов изменения ОП являются необратимые случайные изменения ОП,  вызванные старением, износом или разрегулированием и имеющие определенную зависимость от времени. При этом случайный характер таких изменений обусловлен случайными параметрами, не зависящими от времени. Следовательно, модели реального изменения ОП объекта должны представлять случайные функции, аргументами которых являются постоянные во времени случайные величины и само время.

Рассмотрим наиболее распространенные модели (классы моделей) нестационарных случайных процессов приближения к отказам.

Линейные случайные функции

При линеаризации реального процесса износа объекта каждая реализация Хj (t) процесса заменяется прямой, т. е. реальный процесс изменения ОП Х(t) аппроксимируется случайной функцией вида

(5)

 где Х0 = Х(t=0) = {x}0 - случайное начальное значение ОП (при t = 0), имеющее математическое ожидание (МО)  mxo = M{Х0} и среднее квадратичное отклонение (СКО)  Sxo  = ; V{v} - случайная нормально распределенная скорость изменения ОП во времени, обладающая МО  mv = M{V} и CКО  S v = . Нелинейные случайные функции

Для многих объектов типична некоторая постоянная относительная скорость изменения ОП

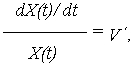
 что соответствует нелинейному случайному процессу Х(t), аппроксимируемому случайной функцией вида

(6)

 где Х0 = Х(t=0) = {x}0 - как и ранее, случайное начальное значение ОП;  V'   - случайная, нормально распределенная скорость изменения натурального логарифма ОП во времени, имеющая МО  mv = M{V }  и СКО  Sv = .

В моделях обоих классов (5) и (6) знаки "+"  и  "-"  используются для аппроксимации соответственно возрастающих и убывающих во времени процессов. Cлучайная величина Х0 в моделях (5), (6) является постоянной во времени, как и случайная величина скорости V изменения ОП в модели (5). В модели (6) постоянной во времени является скорость изменения логарифма ОП, сам же ОП имеет переменную во времени скорость изменения.

В дальнейшем  для простоты обозначения будем полагать, что 

Для удобства дальнейшего рассмотрения моделей  только в линейном варианте модель (6) путем логарифмирования преобразуем к линейной модели изменения логарифма ОП:

(7)

 Обозначая натуральный логарифм ОП случайной функцией Y(t)

(8)

 выражение (7) можно представить в виде

(9)

 подобном модели (5).

Рассмотрим раздельно каждый тип линейных случайных моделей, аппроксимирующих случайный процесс изменения ОП  Х(t) или его логарифма  Y(t).

< Предыдущая		Следующая >