08. Примеры равномощных множеств

Приведенные выше примеры и теоремы показывают, что установить равномощность различных множеств далеко не просто. В этом параграфе мы рассмотрим примеры построения биекции между различными множествами. Будут приведены примеры доказательств равномощности ряда множеств.

Пример 1. Установить биекцию между отрезком [0, 1] и отрезком [а, в].

Решение. Легко устанавливается биективность линейного отображения x = (в – a)t + a отрезка [0, 1] на отрезок [а, в].

Пример 2. Установить биекцию между интервалом (0, 1) и интервалом (–¥, +¥).

Решение. Легко устанавливается биективность отображения x= ctg(pt) интервала (0, 1) на интервал (–¥, +¥).

Задача. Рассмотреть основные элементарные функции и найти промежутки, на которых они являются биективным отображением.

Пример 3. Построить биекцию между отрезком [0, 1] и интервалом (0, 1).

Решение. Решение этой задачи основано на несчетности рассматриваемых множеств и теореме 4 из параграфа 6. Идея решения состоит в том, что из интервала (0, 1) выделяют некоторое счетное множество А. Затем к нему добавляют две точки {0} и {1}. Вновь полученное множество (обозначим его В Ì [0, 1]), также является счетным. Следовательно, множества А и В равномощны и существует биекция f, отображающая B на A. Построим теперь биекцию отрезка [0, 1] на интервал (0, 1) следующим образом:

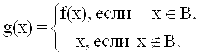
Пример 4. Построить биекцию между окружностью единичного радиуса и отрезком [0, 1].

Схема решения. Легко устанавливается биекция между точкой окружности и углом, соответствующим этой точке. Этим получается биекция окружности и полуотрезка [0, 2p). Затем по схеме примера 3 строится биекция полуотрезка [0, 2p) на отрезок [0, 1].

Пример 5. Доказать, что множество всех окружностей на плоскости, радиусы которых рациональные числа и координаты центра которых - рациональные числа, есть счетное множество.

Решение. Нетрудно видеть, что каждый элемент рассматриваемого множества может быть отождествлен с тройкой чисел (х, у, r), где (х, у) - координаты центра окружности, а r - ее радиус. Этим между множеством указанных окружностей и множеством Q´Q´Q устанавливается биекция. Но произведение счетных множеств счетно (см. задачу в 6 параграфе) и, следовательно, наше множество также счетно.

Пример 6. Доказать, что множество точек разрыва монотонной функции, заданной на отрезке [а, в], конечно или счетно.

Решение. Предположим, что рассматриваемая функция F(Х) является возрастающей. Пусть ХA точка разрыва этой функции. В силу монотонности функции и ее ограниченности ( F(а) < F(Х) < F(в) ) в точке ХA будет существовать как предел слева, так и предел справа: Таким образом, множество точек разрыва { ХA } может быть отождествлено с множеством отрезков{[Aa, Ba]}. При этом необходимо заметить, получаемые отрезки могут пересекаться лишь на концах и все они лежат на отрезке [F(а), F(в)]. Поставим каждому отрезку [Аa, Вa] в соответствие рациональное число уa, выбрав в качестве такового произвольное рациональное число из интервала (Аa, Вa) (наличие такое числа гарантируется аксиомой непрерывности действительных чисел и тем, что Аa ¹ Вa). В силу отмеченного выше, построенное соответствие будет являться инъекцией. Следовательно, мы построили инъекцию множества точек разрыва монотонной функции на отрезке [а, в] в счетное множество рациональных точек отрезка [F(а), F(в)]. Это означает, что рассмотренное множество точек разрыва не более чем счетно.

Задачи.

1. Существует ли функция вида 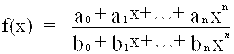(где коэффициенты a0, a1, ..., an; b0, b1, ..., bn - целые числа), обладающая следующим свойством: для любого рационального числа r найдется такое целое число k, что f(k)=r.

2. Найти биекцию числовой прямой на интервал (а, в).

3. Найти биекцию полуотрезка [0, 1) на полуось [0, ¥).

4. Построить биекцию отрезка [0, 1] на всю числовую ось.

5. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на всю числовую ось?

6. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на интервал (с, d)?

7. Установить биекцию между открытым и замкнутым единичным кругом.

8. Какова мощность множества всех треугольников на плоскости, вершины которых имеют рациональные координаты?

9. Какова мощность множества всех рациональных функций с целыми коэффициентами в числителе и знаменателе?

10. Доказать, что множество точек разрыва монотонной функции, определенной на всей числовой прямой, не более чем счетно.

11. Пусть Е - счетное множество точек на прямой. Можно ли так сдвинуть это множество на величину А (т. е. заменить все точки хÎЕ точками х + А), чтобы получившееся в результате сдвига множество ЕA не пересекалось с Е?

12. Пусть Е – счетное множество точек на окружности. Можно ли повернуть окружность вокруг центра на некоторый угол j так, чтобы множество ЕJ, получившееся из Е в результате поворота, не пересекалось с Е?

13. Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше единицы, то множество Е не более чем счетно.

14. Какова мощность множества всех строго возрастающих последовательностей натуральных чисел?

15. Какова мощность множества всех последовательностей натуральных чисел, не содержащих число 7?

16. Какова мощность множества всех многочленов (с произвольными вещественными коэффициентами)?

17. Какова мощность множества всех отрезков на числовой прямой?

18. На числовой прямой задано множество попарно непересекающихся отрезков. Какова его мощность?

19. Какова мощность множества всех строго возрастающих непрерывных функций на отрезке [а, в]?

20. Доказать, что если А – В равномощно В – А, то А и В равномощны.

21. Доказать, что если А Í В и А равномощно АÈС, то В равномощно ВÈС.

22. Верно или нет утверждение: “Если А равномощно С, В равномощно D, причем А Ê В, С Ê D, то А – В равномощно С – D”?

23. Доказать, что множество всех конечных подмножеств счетного множества – счетно.

24. Какова мощность множества всех конечных и счетных подмножеств множества Е, если Е имеет мощность континуума?

< Предыдущая		Следующая >