07. Сравнение мощностей
Теорема 1 (Кантора-Бернштейна). Пусть для множеств А и В существуют множества А1 ÍА и В1 ÍВ такие, что множество А равномощно с В1, а множество В с А1, то множества А и В равномощны.
Доказательство. Пусть f - биекция В на А1, а g - биекция А на В1. Тогда f(В)=А1 и f(В1)=А2 ÍА1. Суперпозиция h=fog функций является также биекцией А на А2. Тогда функция h отображает
А на А2
А1 Í А на А3 Í А
А2 Í А1 на А4 Í А3
А3 Í А2 на А5 Í А6 и т. д.
Отсюда следует, что h является биекцией
Из А – А1 на А2 – А3
Из А1 – А2 на А3 – А4
Из А2 – А3 на А4 – А5 и т. д.
Зададим множества
Е = (А – А1)È(А2 – А3)È(А4 – А5)È(А6 – А7)È ...
F = (А2 – А3)È(А4 – А5)È(А6 – А7)È ...
D = АÇА1ÇА2ÇА3ÇА4Ç...
G = (А1 – А2)È(А3 – А4)È(А5 – А6)È ...
Из замеченного выше следует, что h является биекцией E на F. Кроме того, справедливы равенства А = DÈGÈE и А = DÈGÈF. Следовательно отображение Т из А в А1, определяемое соотношением

Является биекцией А на А1, т. е. множества А и А1 равномощны. Последнее означает, что все четыре множества в теореме равномощны.
Теорема 2. Пусть Х и У два множества такие, что Х¹Æ, У¹Æ и в У не менее двух элементов. Тогда множество всех функций, действующих из Х в У является множеством, мощность которого больше мощности множества Х.
Доказательство. Обозначим множество функций, действующих из Х в У через УХ. Доказательство разобьем на две части. Сперва покажем, что существует инъекция множества Х на часть множества УХ. Пусть у1ÎУ, у2ÎУ, у1 ¹ у2 и х0ÎХ. Построим функцию f[х0] следующим образом: f[х0](х0) = у1, а если х ¹ х0, то f[х0] (х) = у2. При таком построении различным элементам в Х соответствуют различные функции. Например, если х1 ¹ х0, то f[х1](х0) = у2. Таким образом, получаем инъекцию из Х в УX.
Покажем теперь, что не существует биекции между Х и УX. Предположим противное, что g является биекцией из Х на УX и g(x) = fx ÎУХ. Покажем, что существует fÎУХ такое, что f ¹ fх для любого хÎХ. Пусть хÎХ и fхÎУХ соответствующая функция. Определим f(х) = аÎУ из условия а ¹ fх(x). Такой элемент а в У обязательно найдется, т. к. в У не менее двух элементов. Таким образом построенная функция f не будет совпадать ни с одной функцией f. Следовательно g не может быть биекцией.
Теорема 3. Множество всех подмножеств произвольного непустого множества Х имеет мощность большую, чем мощность множества Х.
Доказательство. Положим У={0,1}. Рассмотрим множество УХ. Если fÎУХ, то f разбивает Х на два множества: Х0(f) = {xÎX: f(x)=0} и Х1(f) = {xÎX: f(x) = 1}. Таким образом, каждому fÎУX соответствует множество Х1(f). Наоборот, если Х1 - некоторое подмножество из Х, то полагая
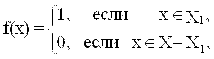
Получим fÎУХ. Этим мы построили биекцию между множеством всех подмножеств множества Х и множеством УХ. Следовательно они равномощны и по теореме 2 мощность множества Х меньше мощности множества всех подмножеств.
Задачи.
1. Пусть А и В произвольные конечные множества, card(А)=n, card(В)=m. Доказать, что общее число отображений из А в В равно nm.
2. Пусть в условиях предыдущей задачи m³n. Определить число биекций и инъекций из А в В.
| < Предыдущая | Следующая > |
|---|