17. Примеры решения задач

Задача 1. В составе Думы представлены 3 партии (по 100, 150, 50 человек от 1-й, 2-й и 3-й партий соответственно). Кандидата на должность спикера Думы поддерживают 50% представителей первой партии, 70% - второй партии и 10% - третьей партии. Какова вероятность того, что наудачу выбранный член Думы поддерживает выдвинутую кандидатуру на должность спикера Думы?

Решение: Из условий задачи очевидно, что с рассматриваемым событием A={наудачу выбранный представитель думы поддерживает выдвинутую кандидатуру} тесно связаны три гипотезы: {Выбранное лицо представляет первую партию}; {выбранное лицо представляет вторую партию}; {выбранное лицо представляет третью партию}. Вероятности этих гипотез сразу определяются из условия задачи: Условные вероятности события А даны в условии задачи: Вероятность события А вычисляем по формуле полной вероятности: Ответ: 0,7.

Задача 2. Страховая компания разделяет застрахованных по трем классам риска: 1 класс – малый риск, 2 класс – средний, 3 класс – большой риск. Среди всех клиентов компании 50% - первого класса риска, 30% - второго и 20% - третьего. Вероятность наступления страхового случая для первого класса риска равна 0.01, второго – 0.03, третьего – 0.08. Какова вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе малого риска?

Решение. Пусть событие А означает, что клиент компании получил вознаграждение. Понятно, что событие А может наступить лишь совместно с одним из трех попарно несовместных событий: - клиент относится к первому классу риска; - клиент относится ко второму классу риска; - клиент относится к третьему классу риска. Необходимо определить условную вероятность Из условия задачи известны вероятности гипотез: Известны также условные вероятности: Искомую вероятность вычисляем по формуле Байеса, т. е.

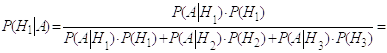
Ответ: 5/19.

< Предыдущая		Следующая >