9.4. Решение уравнения эллиптического типа
Задача Дирихле для уравнения Пуассона
 =F(X,Y) (9.13)
=F(X,Y) (9.13)
Заключается в нахождении функции U=U(X,Y), удовлетворяющей данному уравнению (9.13) внутри некоторой области G={0 < X< A, 0 < Y< B}, а на границе этой области Г - заданному условию:
U|Г=J(M),
Где J - известная функция, M – точка контура Г. Считаем, что задача имеет единственное решение в области с границей Г, и это решение непрерывно в области со своими производными до четвертого порядка включительно.
Выберем прямоугольную сетку, положив:
Xm=m h, m = 0,1,…,M, h = a/M>0,
yn=n l, n = 0,1,…,N, l=b/N>0.
Для аппроксимации уравнения (9.13) используем пятиточечный шаблон. Запишем разностную схему для задачи Дирихле:
Lh(Uh ) = f(h), (9.14)
Где
Lh(Uh )º
И правая часть
F(H)º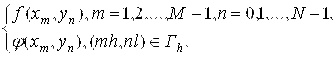
Разностная схема (9.14) представляет собой систему линейных алгебраических уравнений. Число уравнений этой системы равно (M-1)х(N-1), столько же неизвестных Um N, M=1,…,M-1, N=1,…,N-1. Разностная схема устойчива и аппроксимирует данную задачу с погрешностью порядка О(h2). Для решения подобных систем линейных алгебраических уравнений, определяемых формулой (9.14), разработан метод матричной прогонки.
| < Предыдущая | Следующая > |
|---|