9.3.4. Задание

1. Используя разностные аналоги производных, получить для своего варианта разностную схему и найти решение смешанной задачи для дифференциального уравнения параболического типа (теплопроводности).

2. Исследовать схему на аппроксимацию и устойчивость.

Варианты

1. ; U(x,0)=x; U(1,t)=1+t; U(2,t)=2-t; h=0,1; T=1.

2. ; U(x,0)=x2; U(0,t) = t; U(1,t)=1+ t; h=0,1; T=1.

3. ;U(x,0)=x+1; U(0,t)=1; U(1,t)=2+t2; h=0,1; T=1.

4. ; U(x,0)=x2; U(0,t)=0; U(1,t)=1; h=0,1; T=1.

5. ; U(x,0)=x+1; U(0,t)=1; U(1,t)=2+t2; h=0,1; T=1.

6. ; U(x,0)=x2; U(0,t)= t; U(1,t)=1+t; h=0,1; T=1.

7. 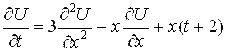;U(x,0)=x+1; U(0,t)=1; U(1,t)=2+t2; h=0,1; T=1.

8. 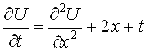;U(x,0)=(1,1x2+1,2) sin(P x); U(0,t)=0; U(2,t)=0; h=0,1; T=1.

9. ; U(x,0)=x+1; U(0,t)=1; U(1,t)=2+t2; h=0,1; T=1.

10.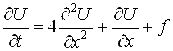; U(x,0)=(1,3x2+1,2 )sin(PX); (0,t)=0;(1,t)=0; h=0,1; T=1.

< Предыдущая		Следующая >