9.3.3. Реализация метода разностной прогонки для уравнения параболического типа
Рассмотрим задачу на примере краевой задачи (9.7). Выберем равномерную прямоугольную сетку, определим узлы по правилу:
Xm=m h, m = 0,1,…,M, h = 1/M>0,
tn=n T, n = 0,1,…,N, T >0, NT £ T < (N+1) T .
Будем использовать неявную разностную схему (9.9), которая аппроксимирует задачу (9.7) с погрешностью O(t+h2) и является абсолютно устойчивой.
Положим в (9.9) N=0, получим:
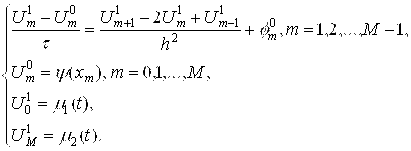
Перепишем в следующем виде, обозначив :
s ![]() - (1+2s)
- (1+2s) ![]() + s
+ s ![]() =-T
=-T![]() -
-![]() , M=1,2,…,M-1, (9.10)
, M=1,2,…,M-1, (9.10)
![]() (0 £ M £ M) - искомое решение задачи на первом слое по времени.
(0 £ M £ M) - искомое решение задачи на первом слое по времени.
Предположим, что между соседними значениями этого решения существует связь:
![]() =AI
=AI![]() +BI, i=0,1,…,M-1, (9.11)
+BI, i=0,1,…,M-1, (9.11)
Где AI , BI - некоторые числовые коэффициенты. При I=0 определим A0, B0 Таким образом, чтобы выполнялось левое граничное условие ![]() =M1(T). Для чего достаточно положить A0=0, B0=M1(T). Возьмем I=M-1. Значение
=M1(T). Для чего достаточно положить A0=0, B0=M1(T). Возьмем I=M-1. Значение ![]() , определяемое по формуле
, определяемое по формуле ![]() =AM-1
=AM-1![]() +BM-1, Подставим в (9.10) и преобразуем опять к виду (9.11), получим вид прогоночных коэффициентов AM , BM:
+BM-1, Подставим в (9.10) и преобразуем опять к виду (9.11), получим вид прогоночных коэффициентов AM , BM:
AM = , BM=
, BM=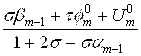 , M=1,…,M-1 . (9.12)
, M=1,…,M-1 . (9.12)
Определение прогоночных коэффициентов по формулам (9.12) для M=1,…,M-1 Называется Прямым ходом метода прогонки. По условию задачи ![]() . Обратный ход метода прогонки Заключается в вычислении значений функции U1I , для I=M-1,M-2,…,1 По формуле (9.11). Далее переходим на следующий слой по времени и т. д.
. Обратный ход метода прогонки Заключается в вычислении значений функции U1I , для I=M-1,M-2,…,1 По формуле (9.11). Далее переходим на следующий слой по времени и т. д.
| < Предыдущая | Следующая > |
|---|