9.4.1. Метод матричной прогонки

Запишем разностную схему (9.14) в виде:

Um+1 N - 2Um N + Um-1 N+A (Um N+1-2Um N+Um N-1 )=H2F(Xm,Yn), (9.15)

M=1,2,…,M-1; n=1,2,…,N-1;

U0n=J(0,yn); Umn=J(a, yn); n=1,2,…,N-1

Um0=J(xm,0); Umn=J(xm, b); m=1,2,…,M-1, где A=h2/l2>0.

Введем обозначение :

Um =(Um 1, Um 2,…, Um N-1)T, M=1,…,M. (9.16)

Положим в формулах (9.15) N=1,2,…,N-1 и, используя (9.16), запишем систему уравнений (9.15) в векторной форме :

Um+1+AUm+Um-1=fm , m = 1,2,…, M-1 (9.17)

U0=J0; UM=JA ,

Где A – трехдиагональная матрица порядка M-1 C диагональным преобладанием, т. к. |1+a|>|a|, a>0 .

A=,

Fm = , J0 = , JA = .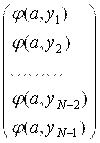

Задача (9.17) аналогична задаче в п.9.3.3, отличие состоит лишь в том, что она имеет векторную форму. Предполагаем, что между соседними значениями векторов этого решения Um существует связь

Uk=RkUk+1+Sk, k=0,1,…,M-1, (9.18)

Где Rk – это матрицы, Sk – векторы.

При K=0 R0=0 U0=J0, S0=J0 - Задано. Возьмем K=M-1 , запишем (9.18) , подставим в (9.17), затем опять преобразуем к виду (9.18). Получим соотношения для вычисления матриц и векторов

Um = -Um+1 (A + Rm-1 )-1 +(Fm - Sm-1 ) (A + Rm-1)-1 , M=1,2,…,M-1.

Вычислим матрицы Rk = - ( A + Rk-1)-1 и векторы Sk= Rk (Sk-1-Fk), Для K=1,..,M-1. Что позволит, используя данное значение вектора на границе UM=JA , вычислить последовательно искомые значения вектора решения по формуле

Um = RmUm+1 + Sm, Для m=M-1,M-2,…,1 .

< Предыдущая		Следующая >