8.3. Методы Рунге-Кутта

Для решения задачи Коши (8.1) семейство Методов Рунге-Кутта описывается следующим выражением:

Y(X+H)=Y(X)+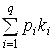 , (8.9)

Где H – шаг сетки; число Q называется порядком точности метода (8.9).

K1=h f(X, y),

k2=h f(X+A2 H, y+B21K1),

…

ki=h f(X+AI H, y+BI1K1+BI2K2+…+BIi-1Ki-1); I=1,…,q.

Здесь Pi, AI , BIk – коэффициенты.

При Q = 1 имеем метод первого порядка точности:

Yi+1=yi+K1,

K1=h f(Xi, yi),

y0=y(x0) .

Метод второго порядка точности (при Q = 2) имеет вид:

Yi+1=yi +(K1+ k2),

K1=h f(Xi, yi),

k2=h f(Xi+h, yi+k1),

y0=y(x0) .

Наиболее распространен на практике метод четвертого порядка точности (при Q=4):

Yi+1=yi+ (K1+2(K2+k3)+k4),

Где K1=H F(Xi, Yi),

K2= h f(Xi+h/2, yi+ k1 /2),

k3= h f(Xi+h/2, yi+ k2 /2),

k4= H F(Xi+ H , Yi+ K3) .

Для нахождения решения с заданной точностью E, Численная реализация методов Рунге-Кутта выполняется следующим образом: задается сетка Xi=A+Ih0, I =1,…,N; H0=(B-A)/N, далее на каждом I -М шаге в точке X=Xi вычисляют два значения Yi(1) и Yi(2):

Yi(1)=yi-1+Pj(h0)kj(h0,xi-1,yi-1),

=yi-1+Pj(h1)kj(h1,xi-1,yi-1),

yi(2)= +Pj(h1)kj(h1,xi-1, ), Где H1=h0 /2 .

Если выполнено условие | Yi(1)- Yi(2)| < E , где E - заданная точность, то следующее Yi+1 вычисляется c тем же шагом H0. В противном случае полагают H0=H1, H1=H0 /2.

< Предыдущая		Следующая >