6.7. Итерационные методы вариационного типа
Рассмотрим Канонический вид итерационной схемы (6.3).
Введем понятия Невязки R(K)=A X(K) - F и Погрешности V(K) = D1/2 (X(K)-X*), где X* - точное решение и D - самосопряженный, положительно определенный оператор в вещественном гильбертовом пространстве H.
Назовем W(K) = B-1 R(K) Поправкой.
Будем выбирать параметр TK+1 Из условия минимума нормы погрешности при переходе от одной итерации к другой. Умножим итерационную схему на D1/2 :
D1/2 x(k+1)=D1/2 x(k)-TK+1(D1/2 Ax(k)-D1/2 Ax*),
v(k+1)=v(k)-TK+1(D1/2 A D -1/2 D1/2(x(k)-x*)),
v(k+1)=v(k)-TK+1 C v(k),
Где обозначено C=D1/2 A D -1/2.
Имеем
![]() .
.
Из условия  найдем
найдем 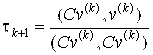 .
.
Рассмотрим следующие методы.
MЕтод скорейшего спуска
Неявная схема: B=B*>0, D=A, А=АT>0.
 .
.
Явная схема: B=E,
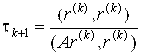 .
.
Метод минимальных невязок
Явная схема: B=E, D=A* A, А>0.
Если A=A*, то D1/2=A И C=A.
v(k+1)=D1/2(x(k)-x*)=A (x(k)-x*)=A x(k)-f = r(k),
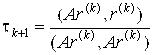 .
.
Метод минимальных поправок
Неявная схема: B=B*>0, D=A* B-1 A, А>0,
 .
.
Метод минимальных погрешностей
Неявная схема: B=(A*)-1B0, D=B0>0, B0= B0T, B0w(k)=A*r(k),
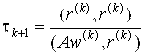 .
.
Явная схема: B=E, A*=B0,
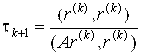 .
.
| < Предыдущая | Следующая > |
|---|