6.8. Методы сопряженных направлений

Рассмотрим схему

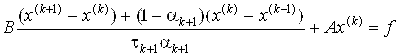. (6.4)

В каноническом виде (6.4) итерационные параметры TK+1 , αK+1 выбираются из условия минимума нормы разрешающего оператора, а не оператора перехода от итерации к итерации.

Запишем итерационные формулы в общем виде:

Где

R(K)=Ax(K) - F – невязка,

W(K)=B-1R(K) – поправка,

Z(K)=X(K) - X* - погрешность,

X* - точное решение.

Если B=E, То схема является явной и имеет вид

Методы сопряженных направлений являются трехслойными и сходятся гораздо быстрее, чем методы вариационного типа. Рассмотрим некоторые из них.

Метод сопряженных градиентов (явная схема): D=A,

.

Метод сопряженных невязок (явная схема): D=A*A,

.

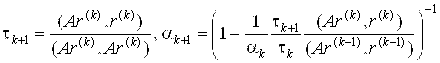Метод сопряженных погрешностей (неявная схема):

D=B0>0, B=(A*)-1B0 ,

< Предыдущая		Следующая >