6.2. Метод Гаусса

Метод Гаусса относится к классу точных методов, т. е. точное решение можно найти за конечное число арифметических операций, в предположении, что нет ошибок округления. В методе Гаусса число арифметических операций равно (2/3)∙M3. Любую матрицу A можно представить в виде произведения верхнетреугольной V И нижнетреугольной L матриц:

A=L∙V.

Если зафиксировать главную диагональ у верхнетреугольной (нижне-треугольной) матрицы, то такое разложение единственно и тогда решение системы можно разбить на два этапа:

- нахождение матриц L И V;

- решение СЛАУ Ly=F и Vx=Y.

Метод Гаусса включает прямой ход - исключения неизвестных, и обратный ход - нахождения решения.

Рассмотрим решение СЛАУ Ax=F , состоящее из N Неизвестных.

(6.2)

Этап I метода Гаусса (Прямой ход метода) сводится к преобразованию исходной матрицы к верхнетреугольному виду, используя пошаговое исключение переменных из системы.

Шаг 1. Разделим первое уравнение на a11≠ 0 , из второго вычитаем первое, умноженное на a21 , из третьего вычитаем первое, умноженное на a31 , и т. д.

Получим

На этом 1- й шаг исключения завершен.

Далее рассмотрим систему:

И аналогичным образом исключим неизвестное X2. Получим систему вида

Таким образом, на каждом K - м шаге будем исключать переменную Xk (K = 1,2,…, N-1) по следующему алгоритму:

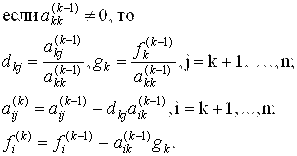
Получим СЛАУ:

Обозначим матрицу коэффициентов V=M(n-1)…M(2)M(1)A, вектор правой части g=M(n-1)…M(2)M(1)f.

Этап II метода Гаусса (Обратный ход метода) состоит в нахождении решения СЛАУ Vx=G из системы с верхнетреугольной матрицей :

,

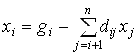, I= N-1, …, 1.

< Предыдущая		Следующая >