2.1. Интерполирование. Постановка задачи интерполирования

Простейшая задача интерполирования заключается в следующем. На отрезке [A, b] заданы N+1 точки X0, x1, …, xn, Которые называются Узлами интерполяции, и значения некоторой функции F(X) в этих узлах:

F(X0)=y0, f(X1)=y1, …, f(Xn)=yn.

Требуется построить функцию F(X) (Интерполирующую функцию), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и F(X):

F(X0)=y0, F(X1)=y1, …, F(Xn)=yn.

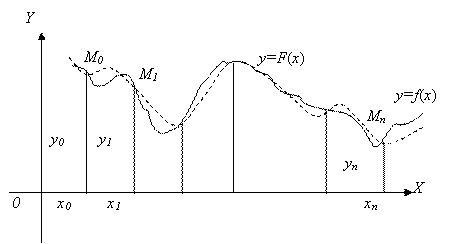
Геометрически это означает, что нужно найти кривую Y=F(X) некоторого определенного типа, проходящую через заданную систему точек Mi(Xi, yi) (I=0, 1, 2, …, n) (см. рис. 2.1).

Функцию F(X) будем искать в виде полинома Pn(X) степени не выше N. Полученную интерполяционную формулу Y=F(X) обычно используют для приближенного вычисления значений данной функции F(X) в точках X, отличных от узлов интерполирования, при этом, если XÎ [X0, xn], то речь идет о задаче Интерполирования, если XÏ [X0, xn] - Экстраполирования.

Рис. 2. 1

< Предыдущая		Следующая >