5.2. Частные производные функции многих переменных

Возрастание (убывание) функции показывает тенденцию изменения функции: функция возрастает (убывает), если с ростом переменной значения функции увеличиваются (уменьшаются). Количественное измерение этих изменений происходит путем вычислений приращений абсолютных, относительных, предельных.

Определение. Абсолютным приращением функции F(X, Y) по переменной х называется разность:

Ясно, что если , то функция на этом промежутке возрастает по Х, если , то убывает.

Определение. Абсолютным приращением функции F(X, Y) по переменной у называется разность:

Определение. Под приращением функции понимают разность:

Где точки (х1, у1) и (х2, у2) из области определения функции.

Определение. Относительное приращение определяется как приращение в расчете на единицу изменения переменной х или переменной у.

Относительное изменение по переменной Х рассчитывается как отношение:

По переменной У:

Пример 35. Пусть дана линейная функция Z=F(X, Y)= - 2X – 2Y + 20.

Рассчитаем прирост функции по Х при переходе из точки (2; 1) в точку (4; 1), т. е. в случае, когда приращение по Х равно 2:

Итак, приращение функции равно –4, т. е. функция Х на интервале изменения переменной Х(2, 4) убывает.

Относительное приращение равно:

Пример 36. Пусть дана функция: Z=F(X, Y)=2X2Y+4Y2.

Прирост функции в точке (2, 3) по переменной У при у=0,5 составляет:

Т. е. по переменной У функция возрастает.

Относительное приращение равно:

Рассмотрим прирост функции по переменной У в точке (2, 4) при у=0,5:

Таким образом, можно заметить, что величина приращения разная для разных У, хотя переменная Х и у одинаковы.

По аналогии с функцией одной переменной определяется непрерывность функции двух переменных.

Определение. Функция F(X, Y) называется Непрерывной в точке (х, у), если приращение функции F стремится к нулю при х0 и у0, т. е., если выполняется условие:

.

Для функций многих переменных, как и в случае функции одной переменной, изучаются предельные значения относительных приращений по отдельным переменным. Так, по переменной Х рассматривается:

 или  при х0.

 Определение. Если существует предел отношения  при х0, то он называется Частной производной первого порядка функции F(X, Y) по х.

Частная производная по Х (у) показывает предельное приращение функции в данной точке (х, у) при  фиксированном У (х).

Анализ предельных изменений функций имеет широкое применение в экономических исследованиях. Например, равенства предельных доходов и предельных затрат, равенства

Удельных предельных полезностей по товарам являются достаточными условиями эффективности принимаемых решений и др.

Функцию U=F(X1, …, хN) можно дифференцировать по каждому из ее аргументов, считая при этом все остальные аргументы постоянными.

Рассмотрим еще одно определение частной производной.

Определение. Производная от функции U=F(X1, …, хN) по х1, взятая в предположении, что все остальные аргументы X2, …, хN являются постоянными, называется Частной производной от U  по X1 И обозначается   Или .

Аналогично определяются и обозначаются частные производные от функции U по каждому из остальных ее аргументов.

Частные производные функции многих переменных находятся по известным правилам дифференцирования функции одной независимой переменной.

Пример 37. Найти частные производные от функции

Решение. Считая Z функцией только одного аргумента Х, находим

Аналогично, считая Z функцией только У, получим

Пример 38. Найти частные производные от функции U(X1, X2, X3)=Sin2(3X1+2X2-X3).

Решение. Считая Х2 И Х3 постоянными, рассмотрим функцию U как функцию одной переменной Х1:

Аналогично находим производные по Х2 и по Х3:

Пример 39. Найти частные производные функции

Решение.

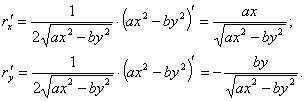
< Предыдущая		Следующая >