4.7. Метод Пауэлла
Этот метод, разработанный Пауэллом, основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схему алгоритма можно описать следующим образом. Пусть Х1 – начальная точка, х – выбранная величина шага по оси Х.
Алгоритм метода Пауэлла:
Шаг 1. Вычислить ![]()
Шаг 2. Вычислить F(X1) и F(X2).
Шаг 3. Если F(X1) > F(X2), положить ![]() Если
Если ![]() Положить
Положить ![]() .
.
Шаг 4. Вычислить F(X3) и найти
![]()
Шаг 5. По трем точкам Х1, х2, х3 Вычислить![]() , Используя формулу оценивания квадратичной аппроксимации:
, Используя формулу оценивания квадратичной аппроксимации:
![]()
Шаг 6. Проверка на окончание поиска.
А) является ли разность ![]() достаточно малой?
достаточно малой?
Б) является ли разность ![]() достаточно малой?
достаточно малой?
Если оба условия выполняются, закончить поиск. В противном случае перейти к шагу 7.
Шаг 7. Выбрать «наилучшую» точку (![]() ) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
Заметим, что при первой реализации шага 5 границы интервала, содержащего точку минимума, не обязательно оказываются установленными. При этом полученная точка ![]() может находиться за точкой Х3 . Поэтому следует провести после шага 5 дополнительную проверку и в случае, когда точка
может находиться за точкой Х3 . Поэтому следует провести после шага 5 дополнительную проверку и в случае, когда точка ![]() находится слишком далеко от Х3, заменить
находится слишком далеко от Х3, заменить ![]() точкой, координата которой вычисляется с учетом заранее установленной длины шага.
точкой, координата которой вычисляется с учетом заранее установленной длины шага.
Пример 22. Минимизировать функцию F(X) = 2X2 + (16/X).
Решение. Пусть начальная точка X1 = 1 и длина шага X = 1. Для проверки на окончание поиска используются следующие параметры сходимости:
![]()
Итерация 1.
Шаг 1. ![]()
Шаг 2. ![]()
Шаг 3. ![]()
Шаг 4.
![]()
Шаг 5. Используя метод параболической аппроксимации, находим
![]()
Шаг 6. Проверка на окончание поиска:

Следовательно, продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.
Итерация 2.
Шаг 4.

Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:

Следовательно, продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 3, которая начинается с шага 4.
Переходим к итерации 3, которая начинается с шага 4.
Итерация 3.
Шаг 4.

Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:
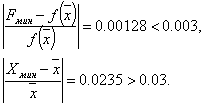
Точность достигнута. Следовательно, поиск закончен.
Получили ![]()
Пример 23. Найти минимальное значение F* и точку минимума Х* функции ![]() . Точку Х* Найти с точностью =0,05.
. Точку Х* Найти с точностью =0,05.
Решение. Пусть начальная точка X1 =3 и длина шага X = 1. Для проверки на окончание поиска используются следующие параметры сходимости:
![]()
Итерация 1.
Шаг 1. ![]()
Шаг 2. ![]()
Шаг 3. ![]()
Шаг 4.
![]()
Шаг 5. Используя метод параболической аппроксимации, находим
![]()
Шаг 6. Проверка на окончание поиска:
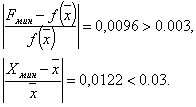
Так как пункт А) Не выполняется, то продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.
Итерация 2.
Шаг 4.
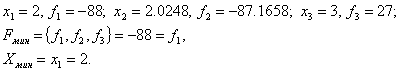
Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:

Следовательно, продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 3, которая начинается с шага 4.
Переходим к итерации 3, которая начинается с шага 4.
Итерация 3.
Шаг 4.

Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:
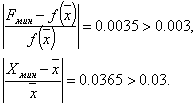
Продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 4, которая начинается с шага 4.
Переходим к итерации 4, которая начинается с шага 4.
Итерация 4.
Шаг 4.

Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:

Условия окончания поиска выполняются, следовательно, вычисления заканчиваем.
Получили ![]()
Пример 24. НАйти точку минимума Х* функции ![]() с точностью =0,05.
с точностью =0,05.
Решение. Пусть начальная точка X1 = 0,5 и длина шага X = 0,2. Для проверки на окончание поиска используются следующие параметры сходимости:
![]()
Итерация 1.
Шаг 1. ![]()
Шаг 2. ![]()
Шаг 3. ![]()
Шаг 4.
![]()
Шаг 5. Используя метод параболической аппроксимации, находим
![]()
Шаг 6. Проверка на окончание поиска:
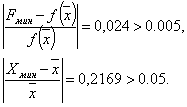
Так как пункт А) Не выполняется, то продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке ![]() Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.
Итерация 2.
Шаг 4.
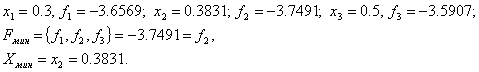
Шаг 5. ![]()
Шаг 6. Проверка на окончание поиска:
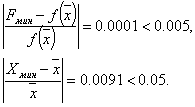
Условия окончания поиска выполняются, следовательно, вычисления заканчиваем.
Получили ![]()
| < Предыдущая | Следующая > |
|---|