4.6. Метод параболической аппроксимации
Метод заключается в замене нелинейной функции F(X) квадратичной параболой F2(X), построенной по трем точкам, принадлежащим F(X), с последующим нахождением максимума (минимума) параболической функции, используя аналитические условия оптимальности: 
На первом этапе в качестве исходных трех точек используется
В этих точках вычисляется F(X) и по полученным точкам F(X1), F(X2), F(X3) строится парабола 
Коэффициенты которой находятся из решения соответствующей системы уравнений: 
Условие оптимальности приводит к уравнению 
Где Х4 – точка максимума (минимума) параболы F2(X). Далее выбирается новый отрезок, внутри которого находится точка Х4, и, используя Х3, Х4, строится новая парабола, по которой уточняется положение максимума (минимума) F(X) и т. д. До тех пор, пока величина отрезка, внутри которого находится оптимум, не будет меньше заданной погрешности . Таким образом, метод имеет итерационный характер.
К достоинству метода относится высокая скорость сходимости, хотя метод может не всегда сходится.
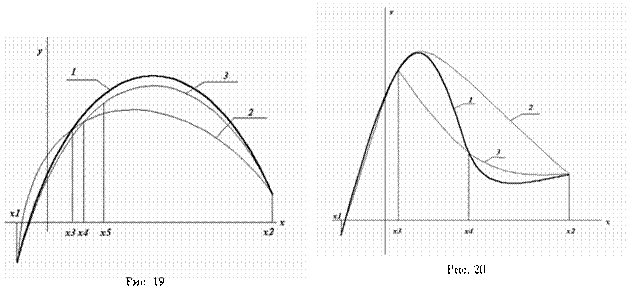
На рис. 19 рассмотрена ситуация, когда метод параболической аппроксимации сходится к решению уже на третьем этапе. Парабола, построенная по точкам Х3, х4, х5, практически совпадает с исходной функцией. На рис. 20 парабола не имеет максимума уже на втором этапе. В первом случае решение найти можно, во втором – нельзя.
Пример 19. Дана функция F(X) = Sin (X + 1). Найти максимум на интервале [-1; 2], точность = 0,01.
Решение. Для построения аппроксимирующей параболы находим точки В первом случае система уравнений для нахождения коэффициентов параболы примет вид:
Решение системы можно найти любым из известных способов, например, по формулам Крамера. На первом шаге получаем 
= 0,5571, F() = 0.9999. По этой точке, а также по второй и третьей исходным точкам, лежащим по обе стороны от точки максимума параболы, аналогично строится вторая парабола.
Таблица 14
|
П
|
X1
|
X2
|
X3
|
F(х1)
|
F(x2)
|
F(x3)
|
C2
|
C1
|
C0
|
|
 |
|
1
|
-1
|
0.5
|
2
|
0
|
0.9975
|
0.1411
|
-0.412
|
0.459
|
0.871
|
0.5571
|
0.9999
|
|
2
|
0.5
|
0.5571
|
2
|
0.9975
|
0.9999
|
0.1411
|
-0.4249
|
0.4914
|
0.858
|
0.5782
|
1
|
|
3
|
0.5571
|
0.5782
|
2
|
0.9999
|
1
|
0,1411
|
-0,4208
|
0.4809
|
0.8626
|
0.5714
|
1
|
|
4
|
0,5571
|
0,5714
|
0,5782
|
0,9999
|
1
|
1
|
-0,5
|
0,5708
|
0,8371
|
0,5708
|
1
|
Поскольку уже на третьем шаге разница между двумя точками максимума менее заданной погрешности, то поиск можно заканчивать (четвертый шаг присутствует для наглядности вычислений).
Поэтому Х* 
0,5708, и F* F (0,5708) = 1.
Для реализации данного метода существует ещё один подход.
Если задана последовательность точек Х1, х2, х3 и известны соответствующие этим точкам значения функции F1, F2, F3, то можно определить постоянные величины А0, а1, а2 таким образом, что значения квадратичной функции
Совпадут со значениями F(X) в трех указанных точках. Перейдем к вычислению Q(X) в каждой из трех заданных точек. Прежде всего, так как
Поскольку
Наконец, при Х = х3
Разрешая последнее уравнение относительно А2, получаем
Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры аппроксимирующего квадратичного полинома достаточно высоко, значит, в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координаты точки оптимума. Напомним, что стационарные точки функции одной переменной определяются путем приравнивания к нулю ее первой производной и последующего нахождения корней полученного таким образом уравнения. В данном случае из уравнения
Можно получить
Поскольку функция F(X) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина окажется приемлемой оценкой координаты точки истинного оптимума Х*.
Видно, что оба подхода отличаются друг от друга только способом вычисления коэффициентов (в первом случае - C0, C1, C2; во втором - А0, а1, а2) квадратичного полинома. Результаты при этом нисколько ни отличаются. Легко убедиться, что для практических вычислений удобнее использовать формулы
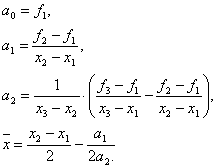
Пример 20. Найти минимальное значение F* и точку минимума Х* функции 
На отрезке [1.5; 2]. Точку Х* Найти с точностью =0,05.
Решение. Значения Х1, х2, х3 находим также как и в предыдущем примере.
Таблица 15
|
П
|
X1
|
X2
|
X3
|
F1
|
F2
|
F3
|
А0
|
А1
|
А2
|
|
|
|
1
|
1,5
|
1,75
|
2
|
-89,4375
|
-92,1211
|
-88
|
-89,4375
|
-10,7344
|
54,4375
|
1,7236
|
-92,1346
|
|
2
|
1,5
|
1,7236
|
1,75
|
-89,4375
|
-92,1346
|
-92,1211
|
-89,4375
|
-12,0623
|
50,2988
|
1,7317
|
-92,1384
|
Уже после второго шага можно закончить вычисления, так как заданная точность достигнута (1,7317-1,7236 = 0,0081 < = 0,05).
Значит, Х* 1,7317, и F* F (1,7317) = -92,1384.
Пример 21. НАйти точку минимума Х* функции 
на отрезке [0.5; 1] с точностью =0,05.
Решение. Вычисления представим в виде табл. 16:
Таблица 16
|
П
|
X1
|
X2
|
X3
|
F1
|
F2
|
F3
|
А0
|
А1
|
А2
|
|
|
|
1
|
0,5
|
0,75
|
1
|
-3,5907
|
-2,4389
|
-0,5
|
-3,5907
|
4,6075
|
6,296
|
0,2591
|
-3,5328
|
|
2
|
0,2591
|
0,5
|
1
|
-3,5328
|
-3,5907
|
-0,5
|
-3,5328
|
-0,2404
|
8,6677
|
0,3934
|
-3,7475
|
|
3
|
0,3934
|
0,5
|
1
|
-3,7475
|
-3,5907
|
-0,5
|
-3,7475
|
1,4708
|
7,7657
|
0,352
|
-3,7373
|
Точность достигнута (0,3934 – 0,352 = 0,414 < = 0,05).
Значит, Х* 0,352, и F* F (0,352) = -3,7373.
| < Предыдущая | Следующая > |
|---|
