22. Вариация функционала

Для дифференцируемой функции (2.18) дифференциал Dy - это главная, линейная относительно Dx, часть приращения функции: 1-е слагаемое формулы (2.18):

(2.27)

Для варьируемого функционала аналогом дифференциала функции будет вариация.

Определение 21. Вариацией dJ(Y) функционала J(Y) на функции Y(X) называется главная, линейная относительно dY, часть его приращения на этой функции ΔJ.

Согласно (2.25) вариация будет линейным относительно dY функционалом. Конечно, вариация будет также зависеть и от той функции Y(X), на которой она вычисляется. Применяя вывод 1', мы можем сказать:

Вывод 7. Если DJ(Y) в Ck, то она существует и в Ck+1.

Как же вычислить вариацию функционала? Здесь возможны различные способы. Мы рассмотрим 2 способа, которые будем применять дальше при исследовании функционалов на экстремум.

1 способ вычисления вариации функционала. Даём бесконечно малое приращение dY функции Y(X) - аргументу нашего функционала. Вычисляем приращение ΔJ, вызванное этой вариацией. Раскладываем его в ряд Тейлора с удержанием только линейных членов.

Этот способ мы будем использовать в следующих главах при выводе дифференциальных уравнений Эйлера. А сейчас рассмотрим 2-й способ, который нам пригодится при выводе необходимого условия экстремума.

2 способ вычисления вариации функционала. Пусть Y0(X) - та функция, на которой нам нужно вычислить вариацию функционала dJ. Рассмотрим класс функций вида

(2.28)

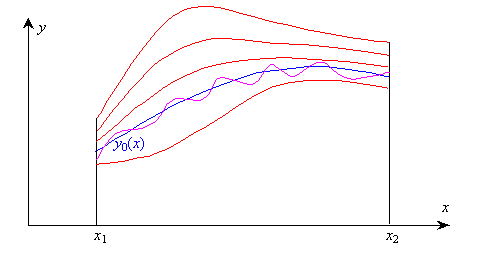
Где a - бесконечно малая величина, а h(X) - фиксированная функция. Этот класс является более узким, чем исходный класс функций: в нём все ординаты меняются пропорционально одному числовому параметру a. На рис.2.7 показана исходная функция Y0(X), несколько функций из класса (2.28) и функция, не принадлежащая классу (2.28).

Рис. 2.7. Функции для 2-го способа вычисления dJ

Мы знаем, что, если существует dJ на каком-либо классе функций, то она существует и на более узком классе. Поэтому по способу 2 мы будем вычислять вариацию функционала на классе функций (2.28). Так как в функциях (2.28) Y0(X) и h(X) - фиксированные, то функционал на функциях вида (2.28) становится фактически функцией одной переменной a:

(2.29)

Причём V(0) соответствует функционалу на исходной функции Y0(X). Найдём приращение функционала:

(2.30)

Так как функционал - варьируемый, то по (2.25) имеем:

(2.31)

Или, с учётом линейности (2.23):

(2.32)

Нам нужно выделить в этом выражении линейный функционал L(Y0,h), это и будет интересующая нас вариация функционала. Для этого разделим обе части (2.32) на a и перейдём к пределу при a→0. В правой части 1-е слагаемое даст интересующую нас величину L(Y0,h). Второе слагаемое стремится к нулю. Действительно, первый множитель |a|/a ограничен по модулю, третий множитель ||h|| - это норма фиксированной функции - также постоянная величина, а вот второй множитель b - это бесконечно малая величина, она стремится к нулю при a→0. Следовательно, предел правой части - это вариация функционала dJ. Найдём предел левой части. В силу (2.30):

(2.33)

Таким образом, вычисление вариации функционала по 2-му правилу сводится к вычислению производной по a от J(Y0+ah) при a=0:

(2.34)

< Предыдущая		Следующая >