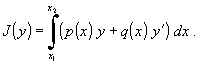21. Непрерывность и варьируемость функционала
Как же исследовать функционал на экстремум? Для этого нужны условия: необходимые - чтобы найти функции, на которых может достигаться экстремум, и достаточные, чтобы проверить: достигается ли экстремум. Для вывода этих условий вновь обратимся к функции N переменных (2.5). Мы знаем, что необходимым условием экстремума такой функции является равенство нулю всех частных производных:
|
|
(2.16) |
Или, что то же самое, равенство нулю полного дифференциала:
|
|
(2.17) |
Разумеется, функция Y(X) при этом должна быть дифференцируемой: её приращение в точке DY должно быть представимо в виде суммы двух слагаемых: линейного относительно вектора малых приращений DX и бесконечно малой величины высшего порядка малости относительно |DX|:
|
|
(2.18) |
Здесь C - вектор постоянных величин (частные производные в точке), b - бесконечно малая величина.
Для того, чтобы мы вообще могли говорить о дифференцируемости, наша функция Y(X) обязательно должна быть непрерывной: бесконечно малому приращению аргументов DX должно соответствовать бесконечно малое приращение функции.
Давайте теперь разбираться с функционалами. Введём понятие, аналогичное понятию дифференциала аргумента, и дадим определение непрерывности функционала.
Определение 16. Вариацией (или приращением) функции Y(X) на функции Y0(X) называется:
|
|
(2.19) |
Вариация называется малой в смысле малости K-го порядка, если её норма в классе Ck мала, т. е. не превышает сколь угодно малого заданного наперёд числа h:
|
|
(2.20) |
Это - аналог бесконечно малого приращения аргумента функции нескольких переменных (дифференциала аргумента). Если вариация dY - малая K-го порядка, то функции Y(X) и Y0(X) и сами отличаются мало, и их производные до K-го порядка включительно также отличаются мало. Однако производные более высокого, например, (K+1)-го порядка порядка, могут уже отличаться значительно. Согласно выводу 2' мы можем утверждать:
Вывод 4. Если вариация dY - малая K-го порядка порядка, то она будет малой и (K-1)-го порядка.
Из (2.19) следует, что операции варьирования и дифференцирования переставимы. Поэтому, когда мы будем писать dY(K), то это означает и d(Y(K)), и (dY)(K).
Вариация функции dY вызывает приращение функционала J.
Определение 17. Приращением функционала J на функции Y0(X), соответствующим вариации функции dY, называется:
|
|
(2.21) |
Будет ли приращение функционала ΔJ малым, если вариация функции - малая? Если да, то мы может сказать, что наш функционал - непрерывный. Дадим точное определение непрерывности.
Определение 18. Функционал J(Y(X)) называется непрерывным на функции Y0(X) в смысле непрерывности K-го порядка, если малой (в смысле малости K-го порядка) вариации функции dY соответствует малое приращение функционала J(Y). Или: функционал J(Y(X)) называется непрерывным на функции Y0(X) в смысле непрерывности K-го порядка, если для любого сколь угодно малого заданного наперёд положительного числа e существует такое малое число h, что, как только мы сделаем норму вариации функции dY (в смысле Ck) меньше h, так сразу модуль приращения функционала станет меньше e.
У Вас не возникает ощущения, что Вы где-то уже это слышали? Конечно, это обычное определение предела. В нашем случае он выглядит так:
|
|
(2.22) |
Здесь норма вариации функции ||dY|| вычисляется в Ck.
Что следует из непрерывности K-го порядка: непрерывность (K-1)-го порядка или (K+1)-го? Как всегда, давайте анализировать. Пусть, например, наш функционал непрерывен в смысле 1-го порядка. Приращение функционала стремится к нулю, когда максимальная из двух величин: max|dY| и max|dY'| стремится к нулю. Если при этом ещё и max|dY''|→0, то хуже от этого не будет: всё равно будет ΔJ→0. А вот если отказаться, например, от требования max|dY'|→0, то оставшегося условия max|dY|→0 может уже оказаться недостаточно для того, чтобы ΔJ→0.
Вывод 5. Если функционал J непрерывен в смысле непрерывности K-го порядка, то он будет непрерывен и в смысле непрерывности (K+1)-го порядка.
С непрерывностью мы разобрались. Далее введём понятие, аналогичное дифференцируемости. Нам нужно будет выделять из приращения функционала главную, линейную часть. Но записать её так, как в (2.18) эта часть записана для функции, мы не можем: у нас нет понятия скалярного произведения. Поэтому введём понятие линейного функционала, а затем используем его в определении варьируемости (это аналог дифференцируемости).
Определение 19. Функционал L(Y) называется линейным, если:
|
|
(2.23) |
Пример линейного функционала:
|
|
(2.24) |
Определение 20. Функционал J(Y) называется варьируемым на функции Y(X), если его приращение на этой функции ΔJ, соответствующее вариации функции dY, можно представить в виде суммы двух слагаемых:
линейного относительно dY функционала L(Y,dY) (этот функционал зависит ещё и от Y - той функции, в окрестности которой вычисляется приращение); бесконечно малого функционала высшего порядка малости по сравнению с dY (мы его можем представить как произведение просто бесконечно малого относительно dY функционала b(Y,dY) на ||dY||):|
|
(2.25) |
Здесь b(Y,dY) - бесконечно малый относительно dY функционал:
|
|
(2.26) |
В определении варьируемости участвует норма вариации функции, поэтому мы должны рассматривать варьируемость в конкретном классе функций, т. е. говорить о варьируемости 0-го, 1-го, ..., K-го порядка. Согласно выводу 1', если функционал варьируемый для всех функций из какого-либо класса, то он будет варьируемым и для всех функций из подкласса этого класса.
Вывод 6. Если функционал J варьируемый в Ck, то он будет варьируемым и в Ck+1.
| < Предыдущая | Следующая > |
|---|