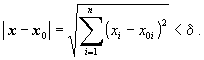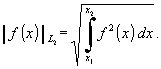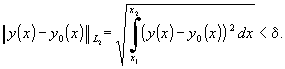19. Классы функций
Давайте вспомним, как мы определяли экстремум функции нескольких переменных
|
|
(2.5) |
Здесь жирным шрифтом обозначен вектор аргументов X.
Определение 4. Точка X0 называется точкой минимума функции Y(X), если эту точку X0 можно окружить некоторой малой d-окрестностью, в которой "X выполняется условие: Y(X)іY(X0). Если при этом "X из этой d-окрестности, кроме X0, будет Y(X)>Y(X0), то говорят, что в точке X0 достигается строгий минимум. Аналогично даётся определение максимума (строгого максимума).
Хотелось бы таким же образом определить экстремум и для функционалов, но что такое d-окрестность функции? Для точки XОRn мы под d-окрестностью точки X0 понимаем N-мерный круг радиуса d с центром в точке X0.
Определение 5. d-окрестность точки X0 – это множество точек X, для которых
|
|
(2.6) |
Здесь Xi – координаты точки X, а X0I – координаты X0.
Правильнее было бы сказать так: мы вначале определили для точки XОRn норму, как квадратный корень из суммы квадратов координат, потом ввели понятие расстояния (норма разности), а затем уже определили d-окрестность точки X0 как такое множество точек, для которых их расстояние до X0 меньше d.
Попробуем пойти по этому же пути для функций. Функцию F(X) на [X1, X2] можно рассматривать как Ґ-мерный вектор: координатные оси – это значения XО[X1, X2], а сами значения координат – это значения функции F(X). Вместо суммы, участвующей в определении 5, мы должны записать интеграл. Тем самым мы определим некоторый класс функций.
Определение 6. Классом функций L2 на [X1, X2] называется множество функций, интегрируемых в квадрате на [X1, X2], для которых норма вычисляется:
|
|
(2.7) |
Если возможны различные толкования, название класса проставляют в виде индекса внизу после определения нормы. Саму норму обозначают не одинарными вертикальными чёрточками, как модуль, а двойными. В определении 6 требуется, чтобы функция была интегрируемой в квадрате на [X1, X2], т. к. там вычисляется такой интеграл.
Используя определение 6, можно ввести понятие d-окрестности функции Y0(X) на классе L2. Это такие функции Y(X), для которых норма разности их от Y0(X) меньше d:
|
|
(2.8) |
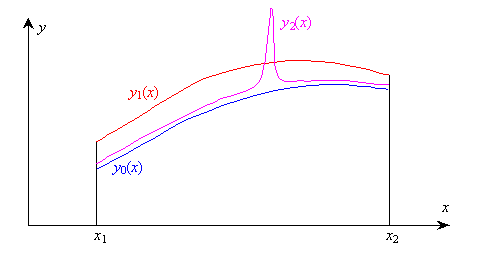
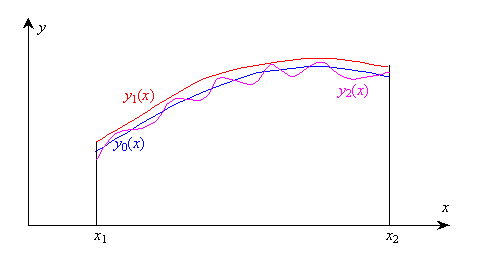
Посмотрите на рис. 2.4. Здесь нарисована исходная функция Y0(X) и ещё две функции: Y1(X) и Y2(X).
|
|
|
Рис. 2.4. Нормы разности функций |
Функция Y2(X) отличается от Y0(X) значительно, но только на небольшом интервале. Наоборот, Y1(X) отличается от Y0(X) во всём интервале [X1, X2]. Площадь между Y1(X) и Y0(X) больше площади между Y2(X) и Y0(X). Поэтому, если вычислять по (2.8) расстояние (норму разности) между Y1(X) и Y0(X), с одной стороны, и Y2(X) и Y0(X) с другой, то окажется, что
|
|
(2.9) |
Функция Y1(X) находится дальше от Y0(X), чем Y2(X).
С классом функций L2 Вы имели дело в теории рядов Фурье. Там, в частности, доказывается, что из всех тригонометрических многочленов степени N наилучшее приближение к функции Y(X) в смысле (2.8) имеет такой многочлен, коэффициенты которого совпадают с коэффициентами Фурье функции Y(X). На этом далее строится доказательство сходимости рядов Фурье.
В вариационном исчислении класс L2 применяется редко. Здесь используются другие классы, которые мы сейчас и рассмотрим.
Определение 7. Классом функций C0 на [X1, X2] называется множество функций, непрерывных на [X1, X2], для которых норма вычисляется:
|
|
(2.10) |
При таком определении нормы две функции Y0(X) и Y(X) считаются близкими, если максимум модуля их разности мал. Так, d-окрестность функции Y0(X) на классе C0 - это такие функции Y(X), для которых норма разности их от Y0(X) меньше d:
|
|
(2.11) |
Посмотрите ещё раз на рис.2.4. Здесь максимальная разность между Y2(X) и Y0(X) больше, чем между Y1(X) и Y0(X). Поэтому, если вычислять расстояние по (2.11), то
|
|
(2.12) |
Функция Y1(X) в смысле C0 находится ближе к Y0(X), чем Y2(X).
Определение 8. Близостью 0-го порядка называется близость в смысле C0.
В (2.11) Y(X) близка к Y0(X) в смысле близости 0-го порядка: норма их разности в C0 мала.
Определение 9. Классом функций C1 на [X1, X2] называется множество функций, дифференцируемых в [X1, X2], для которых норма вычисляется:
|
|
(2.13) |
Близкими в C1 будут такие функции, которые и сами мало отличаются друг от друга, и производные их отличаются мало.
Определение 10. Близостью 1-го порядка называется близость в смысле C1.
|
|
|
Рис. 2.5. Близость в C0 и C1 |
На рис.2.5 функции Y1(X) и Y2(X) мало отличаются от Y0(X) по модулю. Значит, обе они близки к Y0(X) в смысле близости 0-го порядка. Но функция Y2(X) сильно отличается от Y0(X) по значениям производной, а Y1(X) - нет. Поэтому Y1(X) будет близка к Y0(X) в смысле близости 1-го порядка, а Y2(X) - нет. Иными словами, множество функций, близких к данной в смысле близости 1-го порядка, является подмножеством множества функций, близких к данной в смысле близости 0-го порядка. Говорят, что класс C1 является подклассом класса C0. Отсюда следуют 2 важных вывода, которые мы будем далее использовать.
Вывод 1. Если какое-либо свойство выполняется для всех функций из C0, то оно тем более будет выполняться и для всех функций из вложенного в C0 класса C1.
Вывод 2. Если какая-либо функция принадлежит C1, то она тем более будет принадлежать и охватывающему C1 классу C0.
Так, на рис.2.5 Y1(X) близка к Y0(X) в смысле C1 (т. е. принадлежит к множеству функций, близких к Y0(X) в смысле C1). Поэтому она будет также близка к Y0(X) и в смысле C0. Здесь мы применяем вывод 2.2.
А вот обратная ситуация. Пусть мы показали, что какое-то свойство выполняется для всех функций, близких к Y0(X) в смысле C0, т. е. и для Y1(X), и для Y2(X). Тогда в силу Вывода 2.1 это свойство должно иметь место и для всех функций, близких к Y0(X) в смысле C1, в частности, для Y1(X).
Иногда норма в C1 вычисляется не по (2.13), а по формуле:
|
|
(2.14) |
Нетрудно убедиться, что функции, близкие в смысле нормы (2.14), будут также близкими и в смысле (2.13), и наоборот.
Определение 11. Классом функций Ck на [X1, X2] называется множество функций, K раз дифференцируемых в [X1, X2], для которых норма вычисляется:
|
|
(2.15) |
Иногда вместо (2.15) используют формулу, аналогичную (2.14): берут сумму максимумов модулей функции и её производных до K-го порядка включительно.
Близкими в Ck будут такие функции, которые и сами мало отличаются друг от друга, и их производные до K-го порядка включительно отличаются мало.
Определение 12. Близость в смысле Ck называется близостью K-го порядка.
Видно, что класс Ck+1 является подклассом класса Ck: в Ck+1 входят не все функции из Ck, а только та их часть, для которых ещё (K+1)-е производные отличаются мало. Классы C0, C1, ..., Ck вкладываются друг в друга.
Выводы 1 и 2, которые мы сделали для C0 и C1, можно обобщить.
Вывод 1'. Если какое-либо свойство выполняется для всех функций из Ck, то оно тем более будет выполняться и для всех функций из вложенного в Ck класса Ck+1.
Вывод 2'. Если какая-либо функция принадлежит Ck, то она тем более будет принадлежать и охватывающему Ck классу Ck-1.
| < Предыдущая | Следующая > |
|---|