13. Итеративные методы. Постановка задачи
Ограниченные возможности симплексного метода привели к широкому распространению градиентных и других итеративных методов, в основе которых лежит понятие градиента целевой функции g(x).
Градиентом функции g(x), обозначаемым grad g(x) и ![]() , называют вектор, величина которого определяет скорость изменения функции g(x), и наибольшего возрастания этой функции. Пусть
, называют вектор, величина которого определяет скорость изменения функции g(x), и наибольшего возрастания этой функции. Пусть ![]() , но
, но 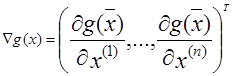 . (1)
. (1)
Условия стационарности точки ![]() . (2) Разложим
. (2) Разложим ![]() в ряд Тейлора в окрестности точки оптимума
в ряд Тейлора в окрестности точки оптимума ![]() , которую считаем стационарной
, которую считаем стационарной ![]() (3), где
(3), где ![]() - отклонение от точки оптимума;
- отклонение от точки оптимума; 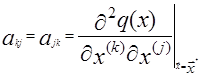 (4), т. к.
(4), т. к. 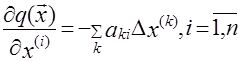 , то
, то
![]() , (5) где элементы матрицы А определяются akj по формуле (4). Разрешая систему уравнений (5) относительно
, (5) где элементы матрицы А определяются akj по формуле (4). Разрешая систему уравнений (5) относительно ![]() , получаем:
, получаем: ![]() . (6) Если заменить неизвестную матрицу А-1 на матрицу Г ([γkj]), то можно надеется, что величина
. (6) Если заменить неизвестную матрицу А-1 на матрицу Г ([γkj]), то можно надеется, что величина ![]() даст значение, более близкое к оптимуму, чем x. При этом открываются возможности многошаговой процедуры поиска.
даст значение, более близкое к оптимуму, чем x. При этом открываются возможности многошаговой процедуры поиска.
Обозначим через ![]() , значение
, значение ![]() на n-ом шаге. Тогда процедура поиска запишется в виде
на n-ом шаге. Тогда процедура поиска запишется в виде ![]() .
.
Градиентный метод.
Этот метод представляет собой последовательность шагов, содержащих две операции:
1) Определение направления наибольшей крутизны спуска, т. е направление антиградиента g(x).
2) Перемещение в выбранном направлении на заданное расстояние.
Математически стратегия градиентного метода получается, если перемещение на каждом шаге ![]() будет пропорционально составляющей градиента в направлении этой оси:
будет пропорционально составляющей градиента в направлении этой оси: ![]() (8) тогда Гn будет диагональной Гn =γI (9) при этом, поправка на n-м шаге равна:
(8) тогда Гn будет диагональной Гn =γI (9) при этом, поправка на n-м шаге равна: ![]() . (10) При таком ограничении некоторые шаги могут оказаться мелкими. Это можно исправить, используя стратегию с постоянным шагом γ.
. (10) При таком ограничении некоторые шаги могут оказаться мелкими. Это можно исправить, используя стратегию с постоянным шагом γ. ![]() (11) где
(11) где ![]() .
.
Метод наискорейшего спуска (подъема).
В этом методе градиент находят только в начальной точке и движении в найденном направлении продолжается c одинаковыми шагами до тех пор, пока уменьшается значение ![]() . Если на каком-то шаге
. Если на каком-то шаге ![]() возросло, то движение в данном направлении прекращается, последний шаг снимается полностью, или на половину, и вычисление нового градиента функции
возросло, то движение в данном направлении прекращается, последний шаг снимается полностью, или на половину, и вычисление нового градиента функции ![]() , т. е новое направление движение.
, т. е новое направление движение.
При этом, шаг движения не должен быть большим, чтобы не пропустить оптимум на данном направлении.
Алгоритм Ньютона.
Этот метод применим, когда поверхность отклика достаточно хорошо описывается уравнением 2-го порядка. Метод позволяет резко уменьшить число шагов. При хорошей поверхности отклика вторые производные: ![]() (12) вычисленные в точки
(12) вычисленные в точки ![]() будут близкими и элементам akj матрицы А. Используя в качестве Гn матрицу вторых производных
будут близкими и элементам akj матрицы А. Используя в качестве Гn матрицу вторых производных ![]() в точке
в точке ![]() , получим вектор поправок для алгоритма Ньютона:
, получим вектор поправок для алгоритма Ньютона: ![]() . (13) Если разложения (3) является точным, то оптимум достигается за один шаг.
. (13) Если разложения (3) является точным, то оптимум достигается за один шаг.
| < Предыдущая | Следующая > |
|---|