14. Элементы динамичного программирования
Характер движения объекта управления описывается системой: 
, 
(1), где 
- переменная состояния, а 
- управления (U
V). За критерий качества управления принимают оценку: 
имеющую физический смысл потерь.
Добавочными могут быть ограничения, накладываемые на количество ресурсов (пределы сужения параметров): 
(3).
Оптимальным называют такое решение UV, при котором для объекта (1), при ограничениях (3) и критерии качества (2) принимает минимальное (максимальное) значение.
Величина 
является функционалом. Обычно задача минимизации (2) заменяют задачей минимизацией: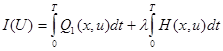 
(4), где λ - множитель Лагранжа.
Докажем возможность такой замены: докажем от противного. Пусть V(t) - управление ≠U(t), такое, что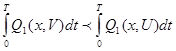 
(5) и выполнено: 
(6), тогда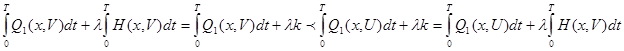 
(7), что противоречит условию, что U(t) обращает (4) в минимум.
Рассмотрим понятие вариации функций. Пусть f(x) непрерывная на [a, b] функция. Рассмотрим значение a < x < b и значение дифференциала Δx=dx. Разность:
F(x+Δx) - f(x) = df(x) = f/(x)Δx есть дифференциал f(x) в точке x. Необходимое условие (минимизации) минимума f(x): df(x)=0.
Рассмотрим значение функции f(x+εΔx) при фиксированных х и Δx оно будет функцией от ε.
(9)
Рассмотрим аналогичные понятия вариационного исчисления. Пусть U(t) и U1(t) - управление. Разность 
(10) называют вариацией функцией U(t), а разность 
(11) называют вариацией функционала.
Вариацию функционала можно определить иначе. Рассмотрим при фиксированных U(t) функционал: 
(12), являющийся функцией ε. Если функционал определён для различных ε, то возможны различные управления 
в близи фиксированного значения U(t). Тогда по аналогии с (9), можно дать определение: 
(13). Если U(t) - оптимальное управление, то функция U(t) будет достигать минимума при ε=0. В этом случае: 
(14), т. е. 
- оптимальное управление – такое при котором вариация функционала обращается в 0.
В вариационном исчислении условие используется для получения дифференциальных уравнений. Эйлера, среди множества решений которого и определяется уравнение U(t), образующие в минимум функционал (4).
| < Предыдущая | Следующая > |
|---|
