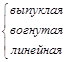12. Ограничения в виде неравенств
1. Обобщённый метод множителей Лагранжа.
Пусть дана задача максимизировать ![]() при ограничениях
при ограничениях ![]() .
.
1) Решить задачу без учёта ограничений. Если полученная точка удовлетворяет все ограничения, то прекратить вычисления, иначе - положить k=1 и продолжить.
2) Сделать любые k ограничений активными (превратить в равенства) и найти оптимум при этих ограничениях. Если найденная точка удовлетворяет оставшимся ограничениям, то локальный оптимум найден. Иначе, увеличим k и повторяем 2). Если все k ограничений были активными, то переходим к 3).
3) Допустимых решений не существует.
2. Условия Кука – Таккера.
Рассмотрим ту же задачу. Ограничения – неравенство можно преобразовать к виду равенств, введя соответствующие неотрицательные переменные ![]() , которые прибавили к левым частям i-x ограничений.
, которые прибавили к левым частям i-x ограничений.
![]() . Пусть
. Пусть ![]() .
.
При этом функция Лагранжа записывается в виде ![]() .
.
В задаче максимизации (минимизации) необходимым условием оптимальности является неотрицательность (неположительность) ![]() .
.
Прировняем частные производные L к 0:
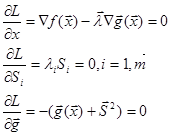
Из этих уравнений следует необходимые условия Кука – Таккера, которые должны удовлетворять ![]() и
и ![]() , определяющие стационарную точку в задаче оптимизации
, определяющие стационарную точку в задаче оптимизации
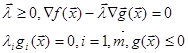
Для минимизации ![]() . Если ограничения заданы в виде равенств, то на знак
. Если ограничения заданы в виде равенств, то на знак ![]() ограничения не накладываются.
ограничения не накладываются.
3. Достаточность условий Кука – Таккера.
Необходимые условия Кука – Таккера являются также достаточными, если целевая функция и область допустимых значений обладают определенными свойствами:
|
Типы оптимизации |
|
|
λI |
|
Максимизация |
Вогнутая |
|
≥0 1 ≤ i ≤ r ≤0 r+1 ≤ i ≤ p без огр. p+1 ≤ i ≤ m |
|
Минимизация |
Выпуклая |
|
≤0 1 ≤ i ≤ r ≥0 r+1 ≤ i ≤ p без огр. p+1 ≤ i ≤ m |
Ограничения задаются в виде:
![]() i = 1,…, r,
i = 1,…, r,
![]() i = r+1,…, p,
i = r+1,…, p,
![]() i = p+1,…, m.
i = p+1,…, m.
Функция Лагранжа:
![]()
4. Квадратичное программирование.
Модель квадратичного программирования определяется, как максимизировать (минимизировать) ![]() при ограничениях
при ограничениях ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Матрица D квадратичной формы предполагается отрицательно (положительно) определённой в задаче максимизации (минимизации). Решение получается путём применения условий Кука – Таккера: ![]() и
и ![]() - множители Лагранжа:
- множители Лагранжа:
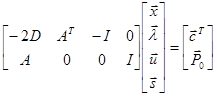 ,
,
Где ![]() - вектор дополнительных переменных.
- вектор дополнительных переменных.
| < Предыдущая | Следующая > |
|---|