11. Ограничения в виде равенств

1) Метод Якоби (приведённого градиента).

Данный метод является обобщенный симплекс метод линейного программирования. Рассмотрим задачу минимизирования z= при ограничениях где , а функция и дважды не прерывно дифференцируемы.

Идея заключается в том, чтобы найти аналитическое выражение для первых частных производных функций , во всех точках удовлетворяющих .

Из теоремы Тейлора следует, что для точки можно записать:

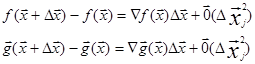
При ∆xj→0 имеем:

Т. к. , то , значит

(1)

Пусть , где являются зависимыми и независимыми переменными (m<n), образующими вектор . Градиенты имеют вид:

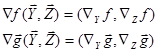
Введём определение двух матрицу:

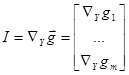(2)

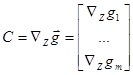(3)

Матрицу называют матрицей Якоби, а матрицей управления.

Перепишем (1):

(4)

Далее: т. к. , то (5)

, (6)

Где - проведенный градиент. Вектор должен обратятся в нуль в стационарных точках. При этом элементы матрицы Гессе соответствуют компонентам вектора независимых переменных . Вектор задаёт i-ю строку матрице Гессе Нс.

2) Метод множителей Лагранжа

Пусть .

Функция L называется функцией Лагранжа, а параметры множителями Лагранжа. Без доказательства приведем утверждение, что в стационарной точке Y0 верно равенство:

Пусть , откуда . Это уравнение выражает условие стационарности точек. В более удобном виде

.

Применительно к функциям Лагранжа эти условия стационарности имеют вид

и .

Это означает, что задача оптимизации при эквивалентна задаче нахождения безусловного экстремума функции Лагранжа .

< Предыдущая		Следующая >