10. Нелинейное программирование

Классическая теория оптимизации основана на использовании дифференциального исчисления для нахождения точек максимума и минимума (экстремумов) функции в условиях наличия и отсутствия ограничений.

Необходимые и достаточные условия существования экстремума.

Рассмотрим условия существования экстремумов функции и переменных , предполагая, что первая и вторая производные непрерывны.

Теорема 1:

Если точка является экстремальной точкой функции , то .

Если - точка максимума (минимума), то (), для всех при малых hj.

По теореме Тейлора при 0≤Θ≤1 верно разложение .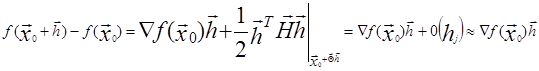

Предположим, что - точка минимума. Предположим, что , тогда для некоторого j 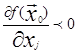, либо .

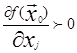Выберем знак так, чтобы 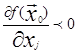, остальные =0. Тогда получим, что , что противоречит определению точки минимума. Значит, .

Это условие является необходимым, но не достаточным. Точки, удовлетворяющие условие будем называть стационарными.

Теорема 2:

Стационарная точка является экстремальной, когда матрица Гессе Н в точки оказывается, определена положительно (т. минимума) или отрицательно (т. максимума).

Из предыдущей теоремы: . Пусть - точка минимума, тогда по определению .

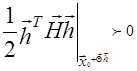Для всех ненулевых , это означает, что , т. к. 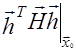- квадратичная форма, то рассматриваемая величина положительна тогда и только тогда, когда - положительно определенная матрица.

Матрица Гессе - матрица с элементами 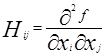. Если неопределенна, то - седловая точка.

Если полуопределена, то в точке может быть экстремум, но для установления этого нужно рассматривать члены разложения в ряд Тейлора более высокого порядка. В некоторых случаях можно сделать вывод об отсутствии экстремума. Сформулируем теорему для f(g) одной переменой.

Теорема 3:

Если в стационарной точке у0 первые (n-1) производные f(y) равны 0, а f(n)(y)≠0, то при y=y0 функция:

1) Имеет точку перегиба, если h - нечетное,

2) Экстремальную точку, если h - четное.

При - максимум, а при - минимум.

< Предыдущая		Следующая >