09. Двойственная задача

Пусть в прямой задаче имеем свободные переменные х1,…, хi и задача сформулирована в виде: максимизировать при условиях: , . (12)

Этой задаче соответствует матрица:

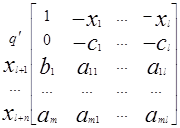(13)

В двойственной задаче за свободные переменные выберем u1,…, um и сформулируем её в виде: минимизировать: (14) при условиях: , . (15). Этой задаче соответствует матрица вида:

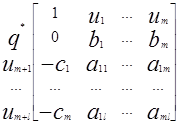(16)

Как видим, матрица (13)- транспонированная матрица (16), значит прямая, и двойственная задача могут быть описаны одной матрицей, однако между прямыми и двойственными переменными должно быть установлено соответствие:

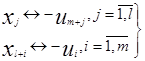. (17)

Если в матрице заданы положительные элементы первой строки, и первого столбца, то матрица соответствует оптимальному решению как прямой, так и двойственной задаче. При этом .

< Предыдущая		Следующая >