09. Игра в смешанных стратегиях

На практике наиболее распространённым является случай, когда платёжная матрица не имеет седловой точки, минимаксные стратегии не оптимальны, каждый из игроков может улучшить своё положение, выбрав вместо одной из чистых стратегий любую из них с заранее заданными вероятностями.

Смешанная стратегия первого игрока – вектор

Р = (р1, р2, ... рm),

Рi – вероятности, с которыми первый игрок называет номера соответствующих строк, т. е. выбирает свои чистые стратегии. Используя Q = (q1,q2, ... qn) – смешанную стратегию, второй игрок выбирает j столбец с вероятностью qj. Из свойств вероятностей событий pi³0 , qj³0, . Случайный выбор игроком своих стратегий называется Смешанной стратегией. Если одна из компонент стратегии равна единице, а остальные нулю, то она является чистой (в противном случае – Смешанной). Чистые стратегии математически описываются единичными векторами

P1=(1,0,0,0...0), Q1=(1,0,0,0...0)

P2=(0,1,0,0...0), Q2=(0,1,0,0...0)

... ... ... ... ... ... ... ... ...

Pm=(0,0,0,0...1) Qn=(0,0,0,0...1)

Тогда в предыдущем примере для первого игрока максиминной является чистая стратегия Р3=(0,0,1), а для второго – чистая стратегии Q3=(0,0,1).

В этом случае каждый из игроков выбирает однозначно с вероятностью равной 1 некоторую стратегию.

Пусть дана платёжная матрица А:

Составляем расширенную матрицу

			Ai
	2	9	2
	6	3	3
Bj	6	9	3 6

Седловой точки не существует, значит, игра имеет решение в смешанных стратегиях. Первый игрок может выиграть не менее 3, второй игрок может проиграть не более 6.

Выбрать свои стратегии игроки должны так, чтобы противник не догадался о них. Игроки чередуют свои стратегии в случайном порядке, причём первый выбирает pi так, чтобы максимизировать наименьший ожидаемый выигрыш по столбцам, а второй игрок выбирает qj так, чтобы минимизировать наибольший ожидаемый проигрыш по строкам. Вероятность выбора первым игроком i-го строки, а вторым j-го столбца равна piqj, игра приобретает случайный характер, случайным является и величина выигрыша.

Средним выигрыш первого игрока при использовании смешанной стратегии P=(p1,p2,...,pn) определяется как математическое ожидание выигрыша первого игрока

(1)

(второй игрок применяет стратегию Q=(q1,q2,...,qn)). Первый игрок старается найти такую стратегию P*, чтобы получить средний выигрыш равный =, a-нижняя цена игры.

i j

Ожидаемый проигрыш по строкам:

Таким образом, первый игрок ориентируется на худшее: оценивает ожидаемый выигрыш как min f. Тогда лучшей будет стратегия P*, позволяющая достичь max min f.

i j

Второй игрок выбирает стратегию дающую b = min max f,

j i

B - верхняя цена игры. Как и в случае чистых стратегий a £ b.

Когда pi и qj соответствуют оптимальным решениям P*, Q*, то a = b = u, где u - цена игры, .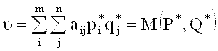

Теорема 2 (основная теорема теории игр). Любая матричная игра имеет решение, т. е. существуют оптимальные стратегии и цена игры.

Поиск оптимальных стратегий начинают с упрощения платёжной матрицы. Строка платёжной матрицы называется Доминируемой, если все её элементы не превосходят соответствующих элементов какой-либо другой строки. Столбец называется Доминирующим, если все его элементы не меньше соответствующих элементов какого-либо другого столбца. Очевидно, что с точки зрения первого игрока не имеет смысла выбирать доминируемую строку, а с точки зрения второго игрока – доминирующий столбец (ими пользоваться заведомо невыгодно). Их можно удалить из платёжной матрицы, что позволяет уменьшить её размерность, а это упрощает решение игры (вероятность применения доминируемых стратегий первым игроком равна 0, вероятность применения доминирующих стратегий вторым игроком равна 0)

Замечание. Оптимальные стратегии в игре с платёжной матрицей и ценой u остаются оптимальными и для игры с платёжной матрицей и ценой . На этом основании платёжную матрицу можно всегда преобразовать так, что её элементы будут неотрицательными числами, что упрощает расчёты.

Пример 4. Выполнить упрощения платёжной матрицы

Решение. Первая строка доминируемая (все её элементы £ соответствующих элементов второй строки), первую строку опускаем:

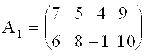
В матрице А1 элементы 3-го столбца меньше соответствующих элементов остальных столбцов, т. е. 1,2 и 4-ый столбцы доминируют над 3-им, их опускаем. Получаем матрицу . Таким образом, наилучшим для первого игрока является чистая стратегия Р2, обеспечивающая ему наибольший выигрыш, =4, а для второго игрока – чистая стратегия Q3, обеспечивающая ему наименьший проигрыш. В данном примере в результате упрощений платёжной матрицы удалось найти решение в чистых стратегиях. Объясняется это тем, что данная платёжная матрица обладает седловым элементом а23 = 4. Таким образом, игра имеет решение в чистых стратегиях

цена игры u=4.

Решение можно найти или графическим способом или свести её к паре симметричных двойственных задач линейного программирования, для решения которых можно использовать, например, симплекс-метод.

< Предыдущая		Следующая >